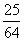题目内容
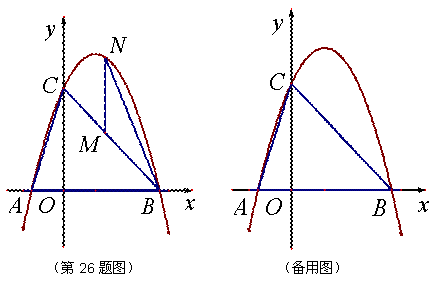
如图，已知抛物线y＝ax2＋bx＋c经过点A（-1，0）、B（3，0）、C（0，3）三点.
（1）、求抛物线相应的函数表达式;
（2）、点M是线段BC上的点（不与B、C重合），过M作MN∥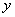
轴交抛物线于N，连接NB. 若点M的横坐标为t，是否存在t，使MN的长最大？若存在，求出sin∠MBN的值；若不存在，请说明理由;
(3)、若对一切x≥0均有ax2＋bx＋c≤mx－m+13成立，求实数m的取值范围．
(1) 用待定系数法，建立方程组正确（2分），抛物线的函数表达式为y=-x2+2x+3（2分）;
(2)MN=-t2+3t=-（t-1.5）2+2.25（2分）;当t=1.5时（1分），MN的最大值为2.25；此时M（1.5，1.5），N（1.5，3.75）；得BM=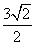
; MN=
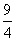; BN=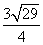
;过点M作△BNM的高MH，得MH=
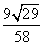（1分）；sin∠MBN=
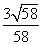（1分）；
（3）令y1=-x2+2x+3； y2=mx－m+13，得直线y2=mx－m+13过点（1，13）（1分），当y1=y2时，有-x2+2x+3=mx－m+13，其△=m2-36=0，得m=-6（2分），或m=6（因为 x≥0，所以舍去），当直线y2=mx－m+13过点C时，m=10（1分），由图像可知，当-6≤m≤10时，均有y1≤y2，所以m的取值范围为-6≤m≤10（1分）。
练习册系列答案
相关题目
的不等式组
的解集为
，则
的值为 ．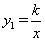 
（k为常数，k≠0）的图象与一次函数
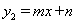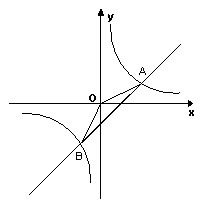
(m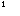 
0)交于点A（2，3）点B（-1，a）．
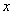在什么范围时，
.
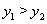，-1，4］ .如果将“特征数”是［2，0，4］的函数图像向左平移3个单位，得到一个新的函数图像，那么这个新图像相应的函数表达式是 ．
法和乘法运算。 已知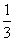
※6的值是
D．
下图是我国几家银行的标志，其中是中心对称图形的有（ ）
|
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
