题目内容
 如图,一人乘雪橇沿坡度为
如图,一人乘雪橇沿坡度为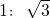 的斜坡笔直滑下,下滑的距离s(米)与时间t(秒)间的关系满足二次函数s=2t2+10t,若滑到坡底的时间为4秒,则此人下降的高度为
的斜坡笔直滑下,下滑的距离s(米)与时间t(秒)间的关系满足二次函数s=2t2+10t,若滑到坡底的时间为4秒,则此人下降的高度为
- A.72米
- B.36米
- C.
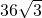 米
米 - D.

B
分析:首先设出下降的高度,表示出水平宽度,利用勾股定理即可求解.
解答: 解:当t=4时,s=10t+2t2=72.
解:当t=4时,s=10t+2t2=72.
设此人下降的高度为x米,过斜坡顶点向地面作垂线,
∵一人乘雪橇沿坡度为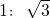 的斜坡笔直滑下,
的斜坡笔直滑下,
∴CA=x,BC= x,
x,
在直角△ABC中,由勾股定理得:
AB2=BC2+AC2,
x2+( x)2=722.
x)2=722.
解得x=36.
故选B.
点评:此题主要考查了二次函数的应用以及坡角问题,理解坡比的意义,应用勾股定理,设未知数,列方程求解是解题关键.
分析:首先设出下降的高度,表示出水平宽度,利用勾股定理即可求解.
解答:
 解:当t=4时,s=10t+2t2=72.
解:当t=4时,s=10t+2t2=72.设此人下降的高度为x米,过斜坡顶点向地面作垂线,
∵一人乘雪橇沿坡度为
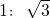 的斜坡笔直滑下,
的斜坡笔直滑下,∴CA=x,BC=
 x,
x,在直角△ABC中,由勾股定理得:
AB2=BC2+AC2,
x2+(
 x)2=722.
x)2=722.解得x=36.
故选B.
点评:此题主要考查了二次函数的应用以及坡角问题,理解坡比的意义,应用勾股定理,设未知数,列方程求解是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图,一人乘雪橇沿坡比1:
如图,一人乘雪橇沿坡比1: 如图,一人乘雪橇沿坡度为
如图,一人乘雪橇沿坡度为 如图,一人乘雪橇沿坡比1:
如图,一人乘雪橇沿坡比1: 的斜坡笔直滑下72米,那么他下降的高度为 米.
的斜坡笔直滑下72米,那么他下降的高度为 米.
 的斜坡笔直滑下72米,那么他下降的高度为 米.
的斜坡笔直滑下72米,那么他下降的高度为 米.