Question

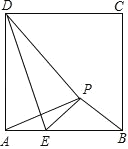
【题目】如图，正方形 ABCD 中，AD＝ ，已知点 E 是边 AB 上的一动点（不与A、B 重合）将△ADE 沿 DE 对折，点 A 的对应点为 P，当△APB 是等腰三角形时， 线段 AE= ．

Answer 1

【答案】2或

【解析】

根据△APB 是等腰三角形可以进行分类讨论：①,此时根据折叠的性质可以得到△APD是等边三角形，则,那么,结合正方形的边长便可以求出;②,此时可以结合等腰三角形的性质进行求解；③,这种情况下是不符合题意得，所以不作考虑；

①当时：

由正方形性质可得：,

由折叠性质可得：

△APD是等边三角形

;

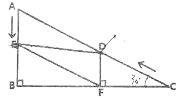
②当时：过P点作于点F,过P点作于点G,如下图所示：

四边形为矩形，

又，

又

在四边形中：

设，那么

由勾股定理可得：

解得：