ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Ν–≤ΡΝœΘ§Άξ≥…œύ”ΠΒΡ»ΈΈώΘΚ
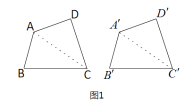
»ΪΒ»ΥΡ±Ώ–ΈΗυΨί»ΪΒ»ΆΦ–ΈΒΡΕ®“εΩ…÷ΣΘΚΥΡΧθ±ΏΖ÷±πœύΒ»Θ§ΥΡΗωΫ«“≤Ζ÷±πœύΒ»ΒΡΝΫΗωΥΡ±Ώ–Έ»ΪΒ».‘ΎΓΑΧΫΥς»ΐΫ«–Έ»ΪΒ»ΒΡΧθΦΰΓ± ±Θ§Έ“Ο«Α―ΝΫΗω»ΐΫ«–Έ÷–ΓΑ“ΜΧθ±ΏœύȖ ΜρΓΑ“ΜΗωΫ«œύȖ≥ΤΈΣ“ΜΗωΧθΦΰ.÷«Μέ–ΓΉιΒΡΆ§―ßάύ±»ΓΑΧΫΥς»ΐΫ«–Έ»ΪΒ»ΧθΦΰΓ±ΒΡΖΫΖ®Θ§ΧΫΥςΓΑΥΡ±Ώ–Έ»ΪΒ»ΒΡΧθΦΰΓ±Θ§Ϋχ––ΝΥ»γœ¬ΥΦΩΦΘΚ»γΆΦ 1Θ§ΥΡ±Ώ–ΈABCDΚΆΥΡ±Ώ–ΈA'B'C'D'÷–Θ§Ν§Ϋ”Ε‘Ϋ«œΏACΘ§A'C'Θ§’β―υΝΫΗωΥΡ±Ώ–Έ»ΪΒ»ΒΡΈ ΧβΨΆΉΣΜ·ΈΣΓΑΓςABCΓ’ΓςA'B'C'Γ±”κΓΑΓςACD Γ’ ΓςA 'C 'D 'Γ±ΒΡΈ Χβ.»τœ»ΗχΕ®ΓΑΓςABCΓ’ΓςA'B'C'Γ±ΒΡΧθΦΰΘ§÷Μ“Σ‘Ό‘ωΦ”2ΗωΧθΦΰ ΙΓΑΓςACDΓ’ΓςA'C'D'Γ±Φ¥Ω…ΆΤ≥ωΝΫΗωΥΡ±Ώ–Έ÷–ΓΑΥΡΧθ±ΏΖ÷±πœύΒ»Θ§ΥΡΗωΫ«“≤Ζ÷±πœύ»ñȧ¥”ΕχΥΒΟςΝΫΗωΥΡ±Ώ–Έ»ΪΒ».
Α¥’’÷«Μέ–ΓΉιΒΡΥΦ¬ΖΘ§–ΓΟςΕ‘ΆΦ1÷–ΒΡΥΡ±Ώ–ΈABCDΚΆΥΡ±Ώ–ΈA'B'C'D'œ»Ηχ≥ω»γœ¬ΧθΦΰΘΚABΘΫA'B'Θ§ΓœBΘΫΓœB'Θ§BCΘΫB'C'Θ§–ΓΝΝ‘Ύ¥ΥΜυ¥Γ…œ”÷Ηχ≥ωΓΑADΘΫA'D'Θ§CDΘΫC'D'Γ±ΝΫΗωΧθΦΰΘ§ΥϊΟ«»œΈΣ¬ζΉψ’βΈεΗωΧθΦΰΡήΒΟΒΫΓΑΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'Γ±.
(1)«κΗυΨί–ΓΟςΚΆ–ΓΝΝΗχ≥ωΒΡΧθΦΰΘ§ΥΒΟςΓΑΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'Γ±ΒΡάμ”…ΘΜ
(2)«κ¥”œ¬ΟφAΘ§BΝΫΧβ÷–»Έ―Γ“ΜΧβΉς¥πΘ§Έ“―Γ‘ώ______Χβ.
A.‘Ύ≤ΡΝœ÷–ΓΑ–ΓΟςΥυΗχΧθΦΰΓ±ΒΡΜυ¥Γ…œΘ§–Γ”±”÷Ηχ≥ωΝΫΗωΧθΦΰΓΑADΘΫA'D'Θ§ΓœBCDΘΫΓœB'C'D'Γ±Θ§¬ζΉψ’βΈεΗωΧθΦΰ_______(ΧνΓΑΡήΓ±ΜρΓΑ≤ΜΡήΓ±)ΒΟΒΫΓΑΥΡ±Ώ–Έ ABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'Γ±.
B.‘Ύ≤ΡΝœ÷–ΓΑ–ΓΟςΥυΗχΧθΦΰΓ±ΒΡΜυ¥Γ…œΘ§‘ΌΧμΦ”ΝΫΗωΙΊ”Ύ‘≠ΥΡ±Ώ–ΈΒΡΧθΦΰ(“Σ«σΘΚ≤ΜΆ§”Ύ–ΓΝΝΒΡΧθΦΰ)Θ§ ΙΓΑΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'Γ±Θ§ΡψΧμΦ”ΒΡΧθΦΰ «ΘΚΔΌ___________ΘΜΔΎ__________.ΘΚ
ΓΨ¥πΑΗΓΩ(1)÷ΛΟςΦϊΫβΈωΘΜ(2)AΧβΘΚ≤ΜΡήΘΜBΧβΘΚΔΌΓœD=ΓœDΓδΘΜΔΎΓœDAC=ΓœDΓδAΓδCΓδ.
ΓΨΫβΈωΓΩ
ΗυΨί»ΪΒ»»ΐΫ«–Έ≈–Ε®Ε®άμ«σΫβΦ¥Ω….
(1)÷ΛΟςΘΚ‘ΎΓςABCΚΆΓςA'B'C'÷–Θ§
ΓΏ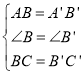
ΓύΓςABCΓ’ΓςA'B'C'(SAS)
ΓύACΘΫA'C'Θ§ΓœBACΘΫΓœB'A'C'Θ§ΓœBCAΘΫΓœB'C'A'Θ§
‘ΎΓςACD ΚΆΓςA'C'D'÷–Θ§
ΓΏ
ΓύΓςACDΓ’ΓςA'C'D'(SSS)
ΓύΓœDACΘΫΓœD'A'C'Θ§ΓœDCAΘΫΓœD'C'A'Θ§ΓœDΘΫΓœD'
ΓύΓœDAC+ΓœBACΘΫΓœD'A'C'+ΓœB'A'C'Θ§ΓœBCA+ΓœDCAΘΫΓœD'C'A'+ΓœB'C'A'
Φ¥ΘΚΓœDABΘΫΓœD'A'B'Θ§ΓœDCBΘΫΓœD'C'B'
ΓΏABΘΫA'B'Θ§BCΘΫB'C'Θ§CDΘΫC'D'Θ§DAΘΫD'A'Θ§
ΓœDABΘΫΓœD'A'B'Θ§ΓœBΘΫΓœB'Θ§ΓœDCBΘΫΓœD'C'B'Θ§ΓœDΘΫΓœD'
ΓύΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'
(2)AΧβΘΚ–ΓΟςΗχ≥ωΒΡΧθΦΰΩ…ΒΟΘΚ‘ΎΓςABCΚΆΓςA'B'C'÷–Θ§
ΓΏ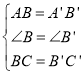
ΓύΓςABCΓ’ΓςA'B'C'(SAS)
ΓύACΘΫA'C'
ΗυΨίADΘΫA'D'Θ§ΓœBCDΘΫΓœB'C'D'Θ§≤ΜΡή≈–Ε®ΓςACDΓ’ΓςA'C'D'
Γύ≤ΜΡήΒΟΒΫΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'
Ι ¥πΑΗΈΣΘΚ≤ΜΡή
BΧβ.–ΓΟςΗχ≥ωΒΡΧθΦΰΩ…ΒΟΘΚ‘ΎΓςABCΚΆΓςA'B'C'÷–Θ§
ΓΏ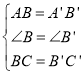
ΓύΓςABCΓ’ΓςA'B'C'(SAS)
ΓύACΘΫA'C'Θ§ΓœBACΘΫΓœB'A'C'Θ§ΓœBCAΘΫΓœB'C'A'Θ§
‘ΎΓςACDΚΆΓςA'C'D'÷–Θ§
ΓΏ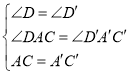
ΓύΓςACDΓ’ΓςA'C'D'(AAS)
ΓύADΘΫA'D'Θ§CDΘΫC'D'Θ§ΓœDCAΘΫΓœD'C'A'.
ΓύΓœDAC+ΓœBACΘΫΓœD'A'C'+ΓœB'A'C'Θ§ΓœBCA+ΓœDCAΘΫΓœD'C'A' +ΓœB'C'A'
Φ¥ΘΚΓœDABΘΫΓœD'A'B'Θ§ΓœDCBΘΫΓœD'C'B'
ΓΏABΘΫA'B'Θ§BCΘΫB'C'Θ§CDΘΫC'D'Θ§DAΘΫD'A'Θ§
ΓœDABΘΫΓœD'A'B'Θ§ΓœBΘΫΓœB'Θ§ΓœDCBΘΫΓœD'C'B'Θ§ΓœDΘΫΓœD'
ΓύΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'
Ι ¥πΑΗΈΣΘΚΓœD=ΓœDΓδΘ§ΓœDAC=ΓœDΓδAΓδCΓδ.

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ



