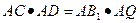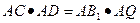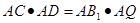Question

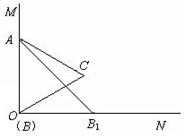
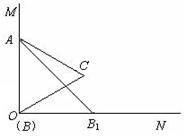
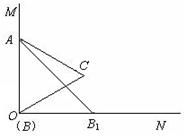
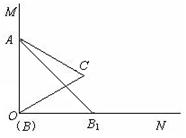
如图，已知∠MON＝90°，等边三角形ABC的一个顶点A是射线OM上的一定点，顶点B与点O重合，顶点C在∠MON内部．

(1)当顶点B在射线ON上移动到B₁时，连结AB₁，请在∠MON内部作出以AB₁为一边的等边三角形AB₁C₁(保留作图痕迹，不写作法和证明)；

(2)设AB₁与OC交于点Q，AC的延长线与B₁C₁交于点D．求证：△ACQ∽△AB₁D；

(3)连结CC₁，试猜想∠ACC₁为多少度？并证明你的猜想．

Answer 1

答案：
解析：

(1)作图如下． 　　(2)证明：∵△AOC与△AB1C1为正三角形， 　∴∠ACB＝∠AB1D＝60°． 　　又∠CAQ＝∠B1AD， 　　∴△ACQ∽△AB1D． 　　(3)猜测∠ACC1＝90°． 　　证明：∵△AOC与△AB1C1为正三角形， 　　∴AO＝AC，AB1＝AC1； 　　∠OAC＝∠C1AB1． 　　又∵∠OAC－∠CAQ＝∠C1AB1－∠CAQ， 　　∴∠OAB1＝∠CAC1，∴△AOB1≌△ACC1， 　　∴∠AOC1＝∠AOB1＝90°．