Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() ”ŕĶ„
”ŕĶ„![]() £¨
£¨![]() £¨
£¨![]() .Ķ„
.Ķ„![]() ī”Ķ„
ī”Ķ„![]() ≥Ų∑Ę£¨‘ŕŌŖ∂ő
≥Ų∑Ę£¨‘ŕŌŖ∂ő![]() …Ō“‘√Ņ√Ž
…Ō“‘√Ņ√Ž![]() ĶńňŔ∂»ŌÚĶ„
ĶńňŔ∂»ŌÚĶ„![]() ‘»ňŔ‘ň∂Į£Ľ”ŽīňÕ¨ Ī£¨īĻ÷Ī”ŕ
‘»ňŔ‘ň∂Į£Ľ”ŽīňÕ¨ Ī£¨īĻ÷Ī”ŕ![]() Ķń÷ĪŌŖ
Ķń÷ĪŌŖ![]() ī”Ķ◊ĪŖ
ī”Ķ◊ĪŖ![]() ≥Ų∑Ę£¨“‘√Ņ√Ž
≥Ų∑Ę£¨“‘√Ņ√Ž![]() ĶńňŔ∂»—ō
ĶńňŔ∂»—ō![]() ∑ĹŌÚ‘»ňŔ∆Ĺ“∆£¨∑÷ĪūĹĽ
∑ĹŌÚ‘»ňŔ∆Ĺ“∆£¨∑÷ĪūĹĽ![]() °Ę
°Ę![]() °Ę
°Ę![]() ”ŕĶ„
”ŕĶ„![]() °Ę
°Ę![]() °Ę
°Ę![]() £¨ĶĪĶ„
£¨ĶĪĶ„![]() ĶĹīÔĶ„
ĶĹīÔĶ„![]() Ī£¨Ķ„
Ī£¨Ķ„![]() ”Ž÷ĪŌŖ
”Ž÷ĪŌŖ![]() Õ¨ ĪÕ£÷Ļ‘ň∂Į£¨…Ť‘ň∂Į Īľšő™
Õ¨ ĪÕ£÷Ļ‘ň∂Į£¨…Ť‘ň∂Į Īľšő™![]() √Ž£®
√Ž£®![]() £©.
£©.
£®1£©ĶĪ![]() Ī£¨Ń¨Ĺ”
Ī£¨Ń¨Ĺ”![]() °Ę
°Ę![]() £¨«ů÷§£ļňńĪŖ–ő
£¨«ů÷§£ļňńĪŖ–ő![]() ő™Ń‚–ő£Ľ
ő™Ń‚–ő£Ľ
£®2£©ĶĪ![]() Ī£¨«ů
Ī£¨«ů![]() Ķń√śĽż£Ľ
Ķń√śĽż£Ľ
£®3£© «∑Ůīś‘ŕń≥“Ľ ĪŅŐ![]() £¨ Ļ
£¨ Ļ![]() ő™“‘Ķ„
ő™“‘Ķ„![]() ĽÚ
ĽÚ![]() ő™÷ĪĹ«∂•Ķ„Ķń÷ĪĹ«»żĹ«–ő£Ņ»Űīś‘ŕ£¨«Ž«ů≥Ųīň ĪŅŐ
ő™÷ĪĹ«∂•Ķ„Ķń÷ĪĹ«»żĹ«–ő£Ņ»Űīś‘ŕ£¨«Ž«ů≥Ųīň ĪŅŐ![]() Ķń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
Ķń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£Ľ£®2£©![]() £Ľ£®3£©īś‘ŕ“‘Ķ„
£Ľ£®3£©īś‘ŕ“‘Ķ„![]() ő™÷ĪĹ«∂•Ķ„Ķń÷ĪĹ«»żĹ«–ő.īň Ī£¨
ő™÷ĪĹ«∂•Ķ„Ķń÷ĪĹ«»żĹ«–ő.īň Ī£¨![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›Ń‚–őĶńŇ–∂®∂®ņŪľīŅ…«ůĹ‚£Ľ
£®2£©”…£®1£©÷™![]() £¨Ļ
£¨Ļ ![]() £¨Ļ
£¨Ļ ![]() £¨Ņ…«ůĶ√
£¨Ņ…«ůĶ√![]() £¨
£¨
![]() £¨ ‘Ŕłýĺ›»żĹ«–őĶń√śĽżĻę ĹľīŅ…«ůĹ‚£Ľ
£¨ ‘Ŕłýĺ›»żĹ«–őĶń√śĽżĻę ĹľīŅ…«ůĹ‚£Ľ
£®3£©łýĺ›Ő‚“‚∑÷ĘŔ»ŰĶ„![]() ő™÷ĪĹ«∂•Ķ„£¨ Ęŕ»ŰĶ„
ő™÷ĪĹ«∂•Ķ„£¨ Ęŕ»ŰĶ„![]() ő™÷ĪĹ«∂•Ķ„£¨ łýĺ›Ōŗň∆»żĹ«–őĶń–‘÷ ľīŅ…«ůĹ‚.
ő™÷ĪĹ«∂•Ķ„£¨ łýĺ›Ōŗň∆»żĹ«–őĶń–‘÷ ľīŅ…«ůĹ‚.
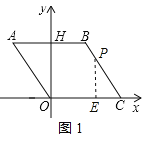
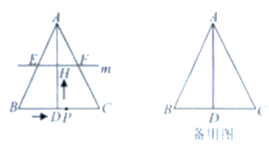
£®1£©÷§√ų£ļ»ÁÕľ1£¨ĶĪ![]() Ī£¨
Ī£¨![]() £¨
£¨
‘Ú![]() ő™
ő™![]() Ķń÷–Ķ„£¨”÷°Ŗ
Ķń÷–Ķ„£¨”÷°Ŗ![]() £¨
£¨
°ŗ![]() ő™
ő™![]() ĶńīĻ÷Ī∆Ĺ∑÷ŌŖ£¨°ŗ
ĶńīĻ÷Ī∆Ĺ∑÷ŌŖ£¨°ŗ![]() £¨
£¨![]() .
.
°Ŗ![]() £¨°ŗ
£¨°ŗ![]() .
.
°Ŗ![]() £¨°ŗ
£¨°ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨°ŗ
£¨°ŗ![]() £¨
£¨
°ŗ![]() £¨ľīňńĪŖ–ő
£¨ľīňńĪŖ–ő![]() ő™Ń‚–ő.
ő™Ń‚–ő.
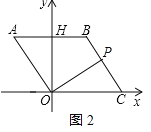
£®2£©»ÁÕľ2£¨”…£®1£©÷™![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨ľī
£¨ľī![]() £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ![]() £¨
£¨
![]() £¨
£¨
![]() £Ľ
£Ľ
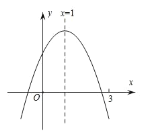
£®3£©ĘŔ»ŰĶ„![]() ő™÷ĪĹ«∂•Ķ„£¨»ÁÕľ3ĘŔ£¨
ő™÷ĪĹ«∂•Ķ„£¨»ÁÕľ3ĘŔ£¨
īň Ī![]() £¨
£¨![]() £¨
£¨![]() .
.
°Ŗ![]() £¨°ŗ
£¨°ŗ![]() £¨
£¨
ľī£ļ![]() £¨īňĪ»ņż Ĺ≤Ľ≥…ŃĘ£¨Ļ ≤Ľīś‘ŕ“‘Ķ„
£¨īňĪ»ņż Ĺ≤Ľ≥…ŃĘ£¨Ļ ≤Ľīś‘ŕ“‘Ķ„![]() ő™÷ĪĹ«∂•Ķ„Ķń÷ĪĹ«»żĹ«–ő£Ľ
ő™÷ĪĹ«∂•Ķ„Ķń÷ĪĹ«»żĹ«–ő£Ľ
Ęŕ»ŰĶ„![]() ő™÷ĪĹ«∂•Ķ„£¨»ÁÕľ3Ęŕ£¨
ő™÷ĪĹ«∂•Ķ„£¨»ÁÕľ3Ęŕ£¨
īň Ī![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() .
.
°Ŗ![]() £¨°ŗ
£¨°ŗ![]() £¨ľī£ļ
£¨ľī£ļ![]() £¨
£¨
Ĺ‚Ķ√![]() .Ļ īś‘ŕ“‘Ķ„
.Ļ īś‘ŕ“‘Ķ„![]() ő™÷ĪĹ«∂•Ķ„Ķń÷ĪĹ«»żĹ«–ő.īň Ī£¨
ő™÷ĪĹ«∂•Ķ„Ķń÷ĪĹ«»żĹ«–ő.īň Ī£¨![]() .
.

 ”¶”√Ő‚◊ų“ĶĪĺŌĶŃ–īūįł
”¶”√Ő‚◊ų“ĶĪĺŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņń≥»Łľĺņļ«Úľ◊A Ń™»Ł≤Ņ∑÷«Ú∂”Ľż∑÷įŮ»ÁŌ¬£ļ
∂”√Ż | Ī»»Ł≥°īő | §≥° | łļ≥° | Ľż∑÷ |
įň“Ľňę¬Ļ | 20 | 18 | 2 | 38 |
ĪĪĺ© ◊ł÷ | 20 | 14 | 6 | 34 |
’„Ĺ≠ÕÚ¬Ū | 20 | 7 | 13 | 27 |
…Ú≤Ņ–Ř ® | 20 | 0 | 20 | 20 |
£®1£©ł√Ī»»Ł §1≥°ĶńĽż∑÷ő™ ∑÷£¨łļ1≥°ĶńĽż∑÷ő™ ∑÷£¨ Ń– ĹĪŪ 弿∑÷”Ž §°Ęłļ≥° ż÷ģľšĶń żŃŅĻōŌĶ£¨ľŔ…Ť §≥° żő™m≥°£¨‘Ú’‚īőĪ»»ŁĶńĽż∑÷ « £®÷ĪĹ”–ī≥ŲĹŠĻŻ£©
£®2£©ń≥∂”Ķń §≥°◊‹Ľż∑÷ń‹Ķ»”ŕňŁĶńłļ≥°◊‹Ľż∑÷¬ū£Ņ