Question

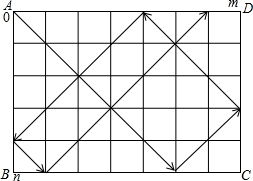
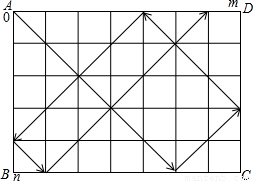
17、一张台面为长方形ABCD的台球桌，只有四个角袋（分别以台面顶点A、B、C、D表示），台面的长、宽分别是m、n（m、n为互质的奇数，且m＞n），台面被分成m×n个正方形．只用一个桌球，从桌角A以与桌边成45°夹角射出，碰到桌边后也以与桌边成45°角反弹（入射线与反射线垂直，如图）．假设桌球不受阻力影响，在落袋前能一直运动．
求证：不论经过多少次反弹，桌球都不可能落入D袋．

Answer 1

分析：首先根据题意作图，然后由m、n均为奇数，分析可得由于桌球从A点以45°角射出，碰到桌边也以45°角反弹，当桌球反弹至邻边时，射线与两边桌边围成一个等腰直角三角形，该等腰直角三角形的斜边两端点也就是球的射线的两端点编号必相同，依次可求得桌球不可能落入的D袋中．

解答：证明：如图：将桌边的正方形顶点从A开始：
按逆时针方向依次编号为0，1，0，1…，0，1，，
∵m、n均为奇数，
∴点B的编号必为1，点C的编号必为0，点D的编号必为1．
由于桌球从A点以45°角射出，碰到桌边也以45°角反弹，
当桌球反弹至邻边时，射线与两边桌边围成一个等腰直角三角形，该等腰直角三角形的斜边两端点也就是球的射线的两端点编号必相同，
（如图中射线EF，等腰Rt△ECF中，∵EC=CF，∴从E经H、C、K到F，编号变为偶数次，E与F的编号必相同）…：
当桌球反弹至对边时，球的射线的两个端点的编号必也相同（如图中射线PG，因为PH=HG=CD，HC+DG，从P经路径ECFD到G，编号也变了偶数次，P与G的编号必也相同）．
综上，不论经过多少次的反弹，桌球在桌边碰到的点的编号均为与A点的编号相同，而A点的编号为0，
所以桌球不可能落入编号为1的D袋中．

点评：此题考查了反射的性质，等腰直角三角形的性质等知识．解题的关键是根据题意画出图形，利用数形结合思想解题．