题目内容
解方程
(1)x2+2x-3=0
(2)3x(x-2)=2(2-x)
(1)x2+2x-3=0
(2)3x(x-2)=2(2-x)
考点:解一元二次方程-因式分解法
专题:计算题
分析:(1)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(2)方程变形后,利用因式分解法求出解即可.
(2)方程变形后,利用因式分解法求出解即可.
解答:解:(1)分解因式得:(x-1)(x+3)=0,
可得x-1=0或x+3=0,
解得:x1=1,x2=-3;
(2)方程变形得:3x(x-2)+2(x-2)=0,
分解因式得:(3x+2)(x-2)=0,
可得3x+2=0或x-2=0,
解得:x1=-
,x2=2.
可得x-1=0或x+3=0,
解得:x1=1,x2=-3;
(2)方程变形得:3x(x-2)+2(x-2)=0,
分解因式得:(3x+2)(x-2)=0,
可得3x+2=0或x-2=0,
解得:x1=-
| 2 |
| 3 |
点评:此题考查了解一元二次方程-因式分解法,熟练掌握因式分解法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某商店积压了一批商品,为尽快售出,该商店采取如下销售方案:将原价每件m元,加价50%,再做两次降价处理,第一次降价30%,第二次降价10%.经过两次降价后的价格n元与原价m元比较( )
| A、原价m高 |
| B、两次降价后的价格n高 |
| C、两个价格相同 |
| D、不能确定 |
 如图,△ACB≌△A1CB1,AB=2,AC=3,BC=4,则A1C的长为( )
如图,△ACB≌△A1CB1,AB=2,AC=3,BC=4,则A1C的长为( )| A、2 | B、3 | C、4 | D、2.5 |
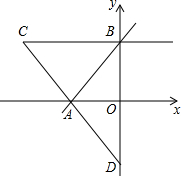 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=