题目内容
完成下面的证明过程
已知:如图,AB∥CD,AE⊥BD于E,CF⊥BD于F,BF=DE.
求证:△ABE≌△CDF.
证明:∵AB∥CD,∴∠1= _________ .(两直线平行,内错角相等 )
∵AE⊥BD,CF⊥BD,
∴∠AEB= _________ =90°.
∵BF=DE,∴BE= _________ .
在△ABE和△CDF中,
∴△ABE≌△CDF _________ .

证明::∵AB∥CD,
∴∠1=∠2(两直线平行,内错角相等),
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∵BF=DE,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA).
故答案为:∠2;∠CFD;DF;∠2,DF,∠CFD;(ASA).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 完成下面的证明过程:
完成下面的证明过程: 12、完成下面的证明过程:
12、完成下面的证明过程: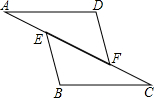 完成下面的证明过程:
完成下面的证明过程: 16、完成下面的证明过程:
16、完成下面的证明过程: 完成下面的证明过程
完成下面的证明过程 