题目内容
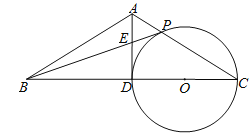
【题目】如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上一点，连接BO交AD于F，OE⊥OB交BC边于点E．
（1）求证：△ABF∽△COE；
（2）当O为AC边中点， 
时，如图2，求
的值；
（3）当O为AC边中点， 
时，请直接写出
的值．
【答案】（1）证明见解析；
（2）
；
（3）
【解析】试题分析：（1）要求证：△ABF∽△COE，只要证明∠BAF=∠C，∠ABF=∠COE即可．（2）作OH⊥AC，交BC于H，易证：△OEH和△OFA相似，进而证明△ABF∽△HOE，根据相似三角形的对应边的比相等，即可得出所求的值．同理可得（3）
=n．
试题解析：（1）
，
．
．
，
，
．
；
（2）作
，交
的延长线于
．
， 
是
边的中点， 
．
由（1）有
， 
， 
．
， 
，
又
， 
． /span>
， 
．
， 
， 
，
， 
．
（3）由（2）得
．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
