题目内容
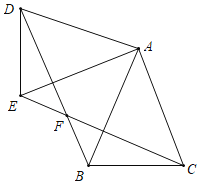
【题目】如图，正方形
的边长为12，点
在边
上，
，过点作
，分别交
、
于
、
两点．若点
、
分别为
、
的中点，则
的长为________．
【答案】
【解析】
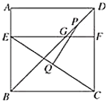
取DF的中点M，连接PM，取CF的中点N，连接QN，作PH⊥QN于点H，然后利用三角形中位线定理、正方形的性质求得PH和QH的长，再根据勾股定理即可解答．
解：取DF的中点M，连接PM，取CF的中点N，连接QN，作PH⊥QN于点H，
∵点
、
分别为
、
的中点，
∴PM=
GF，QN=EF，
∵正方形ABCD的边长为12，点E在边AB上，BE=8，EF∥BC，BD为正方形ABCD的对角线，
∴BE=EG=8，BE=CF=8，
∴GF=4，
∴PM=DM=2，QN=6，FN=CN=4，
∴PH=MN=12－4－2=6，QH=QN-HN=4，
∴PQ=
故答案为：．
练习册系列答案
名校课堂系列答案
相关题目
