题目内容
已知 是一个直角,在角的内部作射线
是一个直角,在角的内部作射线 ,再分别作
,再分别作 和
和 的平分线
的平分线 、
、 .
.

(1)如图①,当 时,则求
时,则求 的度数;
的度数;
(2)如图②,当射线 在
在 内绕
内绕 点旋转时,
点旋转时, 的大小是否发生变化?若变化,说明理由;若不变,求
的大小是否发生变化?若变化,说明理由;若不变,求 的度数.
的度数.
(1)45°;(2)45°
【解析】
试题分析:(1)由AO⊥OB得∠AOB=90°,而∠BOC=60°,则∠AOC=∠AOB-∠BOC=30°,根据角平分线的性质得到∠COE= ∠BOC=30°,∠DOC=
∠BOC=30°,∠DOC= ∠AOC=15°,即可求得结果;
∠AOC=15°,即可求得结果;
(2)由于∠COE= ∠BOC,∠DOC=
∠BOC,∠DOC= ∠AOC,则∠DOE=∠COE+∠COD=
∠AOC,则∠DOE=∠COE+∠COD= (∠BOC+∠AOC),得到∠DOE=
(∠BOC+∠AOC),得到∠DOE= ∠AOB,即可计算出∠DOE的度数.
∠AOB,即可计算出∠DOE的度数.
(1)∵AO⊥OB,
∴∠AOB=90°
又∵∠BOC=60°
∴∠AOC=∠AOB-∠BOC=90°-60°=30°
又∵OD、OE分别平分∠AOC和∠BOC,
∴∠COE= ∠BOC=30°,∠DOC=
∠BOC=30°,∠DOC= ∠AOC=15°,
∠AOC=15°,
∴∠DOE=∠COD+∠COE=30°+15°=45°;
(2)∠DOE的大小不变,等于45°.理由如下:
∵AO⊥OB,
∴∠AOB=90°
∵OD、OE分别平分∠AOC和∠BOC.
∴∠COE= ∠BOC,∠DOC=
∠BOC,∠DOC= ∠AOC,
∠AOC,
∴∠DOE=∠COE+∠COD= (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ∠AOB=
∠AOB= ×90°=45°.
×90°=45°.
考点:角平分线的性质
点评:解答本题的关键是熟练掌握角的平分线把角分成大小相等的两个小角,且都等于大角的一半;注意本题要有整体意识.

学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA ,这时sadA=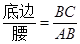 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的. 根据上述关于角的正对定义,解决下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. 根据上述关于角的正对定义,解决下列问题: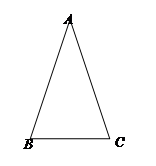
【小题1】sad 的值为( ▲ )
的值为( ▲ )
A.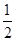 | B.1 | C.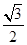 | D.2 |
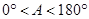 ,∠A的正对值sadA的取值范围是( ▲ )
,∠A的正对值sadA的取值范围是( ▲ )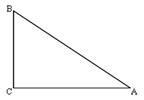
A.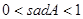 | B.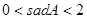 | C.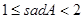 |
D.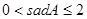 |
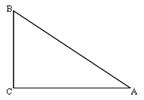
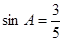 ,AB=25试求sadA的值
,AB=25试求sadA的值 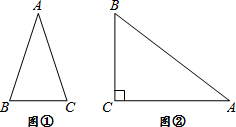 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰= 是一个直角,在角的内部作射线
是一个直角,在角的内部作射线 ,再分别作
,再分别作 和
和 的平分线
的平分线 、
、 .
.
 时,则求
时,则求 的度数;
的度数; 点旋转时,
点旋转时, .容易知道一个角的大小与这个角的正对值也是相互唯一确定的. 根据上述关于角的正对定义,解决下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. 根据上述关于角的正对定义,解决下列问题:
 的值为( ▲ )A.
的值为( ▲ )A. 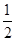 B. 1 C.
B. 1 C. 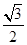 D.
2
D.
2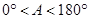 ,∠A的正对值sadA的取值范围是(
▲ )
,∠A的正对值sadA的取值范围是(
▲ )
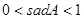 B.
B. 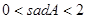 C.
C.
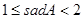
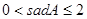
 ,AB=25试求sadA的值
,AB=25试求sadA的值