题目内容
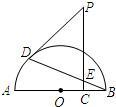
如图①,AB是半圆O的直径,以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D,其中OA=4.
(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接OD,当OD与半圆C相切时,求![]() 的长;
的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.
考点:
圆的综合题.
分析:
(1)AP=PD.理由如下:如图①,连接OP.利用圆周角定理知OP⊥AD.然后由等腰三角形“三合一”的性质证得AP=PD;
(2)由三角形中位线的定义证得CP是△AOD的中位线,则PC∥DO,所以根据平行线的性质、切线的性质易求弧AP所对的圆心角∠ACP=90°;
(3)分类讨论:点E落在线段OA和线段OB上,这两种情况下的y与x的关系式.这两种情况都是根据相似三角形(△APO∽△AED)的对应边成比例来求y与x之间的函数关系式的.
解答:
解:(1)AP=PD.理由如下:
如图①,连接OP.
∵OA是半圆C的直径,
∴∠APO=90°,即OP⊥AD.
又∵OA=OD,
∴AP=PD;
(2)如图①,连接PC、OD.
∵OD是半圆C的切线,
∴∠AOD=90°.
由(1)知,AP=PD.
又∵AC=OC,
∴PC∥OD,
∴∠ACP=∠AOD=90°,
∴![]() 的长=
的长=![]() =π;
=π;
(3)分两种情况:
①当点E落在OA上(即0<x≤2![]() 时),如图②,连接OP,则∠APO=∠AED.
时),如图②,连接OP,则∠APO=∠AED.
又∵∠A=∠A,
∴△APO∽△AED,
∴![]() =
=![]() .
.
∵AP=x,AO=4,AD=2x,AE=4﹣y,
∴![]() =
=![]() ,
,
∴y=﹣![]() x2+4(0<x≤2
x2+4(0<x≤2![]() );
);
②当点E落在线段OB上(即2![]() <x<4)时,如图③,连接OP.
<x<4)时,如图③,连接OP.
同①可得,△APO∽△AED,
∴![]() =
=![]() .
.
∵AP=x,AO=4,AD=2x,AE=4+y,
∴![]() =
=![]() ,
,
∴y=![]() x2+4(2
x2+4(2![]() <x<4).
<x<4).

点评:
本题综合考查了圆周角定理、圆的切线的性质以及相似三角形的判定与性质.解答(3)题时,要分类讨论,以防漏解.解答几何问题时,要数形结合,使抽象的问题变得形象化,降低题的难度与梯度.

 段PC于E,且PD=PE.
段PC于E,且PD=PE.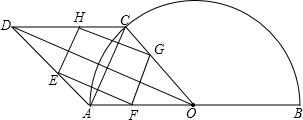 值,判断此时四边形EFGH的形状,并说明理由.
值,判断此时四边形EFGH的形状,并说明理由. 如图,点P是半圆O的直径BA延长线上的动点(不与点A重合),以PO为直径的半圆C与半圆O交于点D,∠DPB的平分线与半圆C交于点E,过E作EF⊥AB于点F,EG∥PB交PD于点G,连接GA.
如图,点P是半圆O的直径BA延长线上的动点(不与点A重合),以PO为直径的半圆C与半圆O交于点D,∠DPB的平分线与半圆C交于点E,过E作EF⊥AB于点F,EG∥PB交PD于点G,连接GA.
