题目内容
某校初三课外活动小组,在测量树高的一次活动中.如图所示,测得树底部中心A到斜坡底C的水平距离为8.8m,在阳光下某一时刻测得l米的标杆影长为0.8m,树影落在斜坡上的部分CD=3.2m,已知斜坡CD的坡比i=1: ,求树高AB.(结果保留整数,参考数据:
,求树高AB.(结果保留整数,参考数据: ≈1.7).
≈1.7).
【答案】分析:过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,根据坡比的定义得到tan∠DCF= ,则∠DCF=30°,根据含30度的直角三角形三边的关系得到DF=
,则∠DCF=30°,根据含30度的直角三角形三边的关系得到DF= CD=1.6m,CF=
CD=1.6m,CF= DF=1.6
DF=1.6 m,所以DE=AC+CF=8.8+1.6
m,所以DE=AC+CF=8.8+1.6 ,再根据三角形相似的性质得到
,再根据三角形相似的性质得到 =
= =
= ,求出BE,即可得到AB.
,求出BE,即可得到AB.
解答: 解:过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,如图,
解:过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,如图,
∵斜坡CD的坡比i=1: ,即tan∠DCF=
,即tan∠DCF= ,
,
∴∠DCF=30°,
而CD=3.2m,
∴DF= CD=1.6m,CF=
CD=1.6m,CF= DF=1.6
DF=1.6 m,
m,
∵AC=8.8m,
∴DE=AC+CF=8.8+1.6 ,
,
∵在阳光下某一时刻测得l米的标杆影长为0.8m,
∴ =
= =
= ,
,
∴BE=11+2 ,
,
∴AB=BE+AE=12.6+2 ≈16m.
≈16m.
答:树高AB为16m.
点评:本题考查了解直角三角形有关坡度的应用:斜坡的坡度等于铅直高度与它对应的水平距离的比值.也考查了相似三角形的性质.
 ,则∠DCF=30°,根据含30度的直角三角形三边的关系得到DF=
,则∠DCF=30°,根据含30度的直角三角形三边的关系得到DF= CD=1.6m,CF=
CD=1.6m,CF= DF=1.6
DF=1.6 m,所以DE=AC+CF=8.8+1.6
m,所以DE=AC+CF=8.8+1.6 ,再根据三角形相似的性质得到
,再根据三角形相似的性质得到 =
= =
= ,求出BE,即可得到AB.
,求出BE,即可得到AB.解答:
 解:过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,如图,
解:过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,如图,∵斜坡CD的坡比i=1:
 ,即tan∠DCF=
,即tan∠DCF= ,
,∴∠DCF=30°,
而CD=3.2m,
∴DF=
 CD=1.6m,CF=
CD=1.6m,CF= DF=1.6
DF=1.6 m,
m,∵AC=8.8m,
∴DE=AC+CF=8.8+1.6
 ,
,∵在阳光下某一时刻测得l米的标杆影长为0.8m,
∴
 =
= =
= ,
,∴BE=11+2
 ,
,∴AB=BE+AE=12.6+2
 ≈16m.
≈16m.答:树高AB为16m.
点评:本题考查了解直角三角形有关坡度的应用:斜坡的坡度等于铅直高度与它对应的水平距离的比值.也考查了相似三角形的性质.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
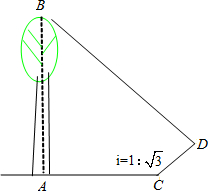 某校初三课外活动小组,在测量树高的一次活动中.如图所示,测得树底部中心A到斜坡底C的水平距离为8.8m,在阳光下某一时刻测得l米的标杆影长为0.8m,树影落在斜坡上的部分CD=3.2m,已知斜坡CD的坡比i=1:
某校初三课外活动小组,在测量树高的一次活动中.如图所示,测得树底部中心A到斜坡底C的水平距离为8.8m,在阳光下某一时刻测得l米的标杆影长为0.8m,树影落在斜坡上的部分CD=3.2m,已知斜坡CD的坡比i=1: ,求树高AB.(结果保留整数,参考数据:
,求树高AB.(结果保留整数,参考数据: ≈1.7).
≈1.7).
 ,求树高AB.(结果保留整数,参考数据:
,求树高AB.(结果保留整数,参考数据: ≈1
≈1 .7).
.7).
 ,求树高AB。(结果保留整数,参考数据:
,求树高AB。(结果保留整数,参考数据: 1.7)
1.7)
 ,求树高AB.(结果保留整数,参考数据:
,求树高AB.(结果保留整数,参考数据: ≈1.7).
≈1.7).