题目内容
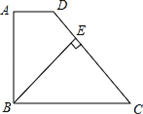
如图，在梯形
中，AD∥BC,BC=4,点
是
的中点，
是等边三角形．
（1）求证：梯形是等腰梯形；
（2）动点
、
分别在线段
和
上运动，且
保持不变．设
求
与
的函数关系式；
（3）在（2）中当取最小值时，判断
的形状，并说明理由．
 |
1）证明：∵是等边三角形
∴
∵是中点
∴
∵
∴
∴
∴
∴梯形是等腰梯形
 |
（2）解：在等边中，
∴
∴
∴
∴
∵
∴
∴
∴
（3）解：为直角三角形
理由是：
∵
∴当取最小值时，
∴是的中点，
而
∴
∴
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
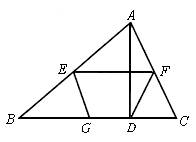
如图，在梯形中ABCD中，AD∥BC，∠ABC=90°，BE⊥CD于点E，AB=BE．
如图，在梯形中ABCD中，AD∥BC，∠ABC=90°，BE⊥CD于点E，AB=BE．