Question

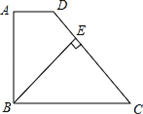
如图，在梯形中ABCD中，AD∥BC，∠ABC=90°，BE⊥CD于点E，AB=BE．
（1）试证明BC=DC；
（2）若∠C=45°，CD=2，求AD的长．

Answer 1

（1）证明：过点D作DF⊥BC于F． 得四边形ABFD是矩形，
∴AB=DF=BE，∠DFC=∠BEC=90°，
在△DFC和△BEC中，
∴△BEC≌△DFC，
∴BC=DC．
（2）解：∵∠DFC=90°，∠C=45°，CD=2，
∴DF=CF，
由勾股定理得：CF²+DF²=CD²=4，
∴，
AD=BF=2﹣．