题目内容
如图所示，点E是正方形ABCD内任一点，把△BEC绕点C旋转至△DFC的位置，∠CFE=________．
45°
分析：判断出△CEF的形状，可得所求角的度数．
解答：由旋转可得：∠ECF=∠BCD=90°，CE=CF，
∴△CEF为等腰直角三角形，
∴∠CFE=45°．
故答案为45°．
点评：考查旋转的性质；根据旋转的性质判断出所求角所在的三角形的形状是解决本题的关键．
分析：判断出△CEF的形状，可得所求角的度数．
解答：由旋转可得：∠ECF=∠BCD=90°，CE=CF，
∴△CEF为等腰直角三角形，
∴∠CFE=45°．
故答案为45°．
点评：考查旋转的性质；根据旋转的性质判断出所求角所在的三角形的形状是解决本题的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
于点Q，连接OQ，当点P沿x轴的正方向运动时Rt△QOP的面积
于点Q，连接OQ，当点P沿x轴正方向运动时，Rt△QOP的面积
于点Q，连接OQ，当点P沿x轴正方向运动时，Rt△QOP的面积
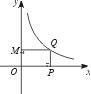
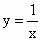于点Q，连接OQ，当点P沿x轴的正方向运动时，Rt△QOP的面积