题目内容
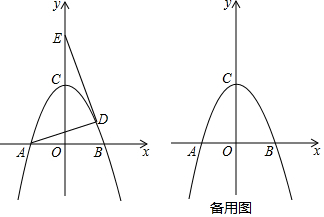
1.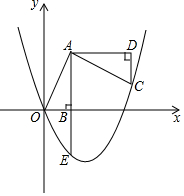 如图,AB⊥x轴于点B,将△ABO绕点A逆时针旋转90°得到△ADC,其中点B与点D是对应点,抛物线y=ax2-$\frac{8}{3}$x经过点C,延长AB交抛物线于点E,已知点A的坐标为(2,4)
如图,AB⊥x轴于点B,将△ABO绕点A逆时针旋转90°得到△ADC,其中点B与点D是对应点,抛物线y=ax2-$\frac{8}{3}$x经过点C,延长AB交抛物线于点E,已知点A的坐标为(2,4)(1)求该抛物线的表达式;
(2)求梯形CDAE的面积.
分析 (1)根据旋转的性质求出点C的坐标,然后将点C的坐标代入抛物线的解析式即可求出答案.
(2)线求出E的坐标,从而可求出AE的长度,根据梯形面积公式即可求出答案.
解答 解:(1)∵A(2,4)
∴OB=2,AB=4,
由旋转的性质可知:AD=AB=4,
CD=OB=2,
∴D(6,4),C(6,2),
将C(6,2)代入y=ax2-$\frac{8}{3}$x,
∴a=$\frac{1}{2}$
∴抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{8}{3}$x,
(2)由于AE⊥x轴,
∴E的横坐标为2,
将x=2代入y=$\frac{1}{2}$x2-$\frac{8}{3}$x,
∴y=-$\frac{10}{3}$
∴E的坐标为(2,-$\frac{10}{3}$),
∴AE=4+$\frac{10}{3}$=$\frac{22}{3}$,
∴S梯形CDAE=$\frac{(CD+AE)•AD}{2}$=$\frac{(2+\frac{22}{3})×4}{2}$=$\frac{56}{3}$
点评 本题考查二次函数的综合问题,涉及待定系数法,梯形面积公式,解方程等知识,本题属于中等题型.

练习册系列答案
相关题目
 如图是由6个大小相同的小正方体组成的几何体,它的主视图是( )
如图是由6个大小相同的小正方体组成的几何体,它的主视图是( )



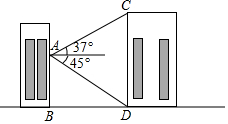 如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m)
如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m)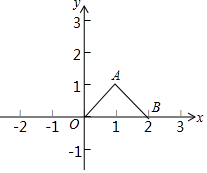 如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(1,1),在x轴上找出点B,使△AOB为等腰三角形,满足条件的点B的坐标为(1,0)或(-$\sqrt{2}$,0)或($\sqrt{2}$,0)或(2,0).
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(1,1),在x轴上找出点B,使△AOB为等腰三角形,满足条件的点B的坐标为(1,0)或(-$\sqrt{2}$,0)或($\sqrt{2}$,0)或(2,0).