题目内容
如图,已知AC是⊙O的直径,MA,MB分别切⊙O于点A,B.
(1)如图1,若∠BAC=25°,求∠AMB的大小;
(2)如图2,过点B作BD⊥AC,交AC于点E,交⊙O于点D,连接AD,若BD=AM=2
.
①求∠AMB的大小;
②图中阴影部分的面积为
π-
π-
.
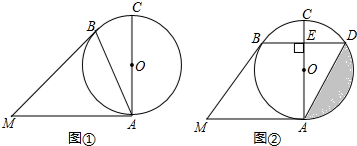
(1)如图1,若∠BAC=25°,求∠AMB的大小;
(2)如图2,过点B作BD⊥AC,交AC于点E,交⊙O于点D,连接AD,若BD=AM=2
| 3 |
①求∠AMB的大小;
②图中阴影部分的面积为
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
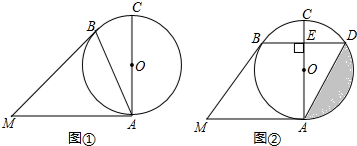
分析:(1)由MA,MB分别切⊙O于点A,B,易得MA=MB,∠MAC=90°,继而求得∠MAB=∠MBA=65°,则可求得∠AMB的大小;
(2)①易证得四边形MADB是菱形,然后由特殊角的三角函数值,求得∠D的度数,继而求得∠AMB的大小;
②首先连接OD,求得∠AOD的度数,OA的长,继而求得答案.
(2)①易证得四边形MADB是菱形,然后由特殊角的三角函数值,求得∠D的度数,继而求得∠AMB的大小;
②首先连接OD,求得∠AOD的度数,OA的长,继而求得答案.
解答:解:(1)∵MA切⊙O于点A,
∴CA⊥AM,
∴∠MAC=90°,
∵∠BAC=25°,
∴∠MAB=90°-25°=65°,
∵MA,MB分别切⊙O于点A,B,
∴MA=MB,
∴∠MAB=∠MBA=65°,
∴∠AMB=180°-(∠MAB+∠MBA)=50°;
(2)①∵MA⊥AC,BD⊥AC,
∴MA∥BD,
∵MA=BD,
∴四边形MADB是平行四边形,
∵MA=MB,
∴?MADB是菱形,
∵AC是⊙O的直径,BD⊥AC,
∴BE=DE,
在Rt△AED中,cos∠ADE=
=
,
∴∠ADE=60°,
在菱形MADB中,∠AMB=∠ADE=60°;
②连接OD,
∵∠ADE=60°,AE⊥BD,
∴∠DAE=30°,
∴∠EOD=60°,
∴∠AOD=120°,
∵DE=
BD=
,AD=BD=2
,
∴AE=
=3,OD=
=2,
∴S阴影=S扇形AOD-S△AOD=
-
×2×
=
π-
.
故答案为:
π-
.
∴CA⊥AM,
∴∠MAC=90°,
∵∠BAC=25°,
∴∠MAB=90°-25°=65°,
∵MA,MB分别切⊙O于点A,B,
∴MA=MB,
∴∠MAB=∠MBA=65°,
∴∠AMB=180°-(∠MAB+∠MBA)=50°;
(2)①∵MA⊥AC,BD⊥AC,
∴MA∥BD,
∵MA=BD,
∴四边形MADB是平行四边形,
∵MA=MB,
∴?MADB是菱形,
∵AC是⊙O的直径,BD⊥AC,
∴BE=DE,
在Rt△AED中,cos∠ADE=
| DE |
| AD |
| 1 |
| 2 |

∴∠ADE=60°,
在菱形MADB中,∠AMB=∠ADE=60°;
②连接OD,
∵∠ADE=60°,AE⊥BD,
∴∠DAE=30°,
∴∠EOD=60°,
∴∠AOD=120°,
∵DE=
| 1 |
| 2 |
| 3 |
| 3 |
∴AE=
| AD2-DE2 |
| DE |
| sin60° |
∴S阴影=S扇形AOD-S△AOD=
| 120π×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
故答案为:
| 4 |
| 3 |
| 3 |
点评:此题考查了切线的性质、切线长定理、勾股定理、垂径定理、菱形的判定与性质以及特殊角的三角函数问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 19、如图,已知AC是⊙O的弦,AB为⊙0的直径,点D在AB的延长线上,∠A=∠D=30°
19、如图,已知AC是⊙O的弦,AB为⊙0的直径,点D在AB的延长线上,∠A=∠D=30° 如图,已知AC是⊙O的弦,AB为⊙0的直径,点D在AB的延长线上,∠A=∠D=30°
如图,已知AC是⊙O的弦,AB为⊙0的直径,点D在AB的延长线上,∠A=∠D=30° .
.
