题目内容
3.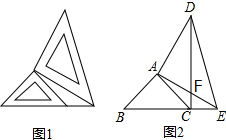 两块不相等的等腰直角三角形如图1放置,图2是它们抽象出的几何图形,点B、C、E在同一条直线上,连接CD,AE、CD交于点F,请你在不添加线段或字母的情况下:
两块不相等的等腰直角三角形如图1放置,图2是它们抽象出的几何图形,点B、C、E在同一条直线上,连接CD,AE、CD交于点F,请你在不添加线段或字母的情况下:(1)找出一对全等三角形并证明;
(2)找出一对相似但不全等的三角形,并证明(△ABC∽△AED除外).
分析 (1)△ABE≌△ACD,理由为:由三角形ABC与三角形AED都为等腰直角三角形,利用等腰直角三角形的性质得到AB=AC,AD=AE,且∠BAC=∠EAD=90°,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)△ADF∽△CEF,理由为:由△ABE≌△ACD,利用全等三角形对应角相等得到∠ADC=∠AEB,再由一对对顶角相等,利用两对对应角相等的三角形相似即可得证.
解答 (1)答:△ABE≌△ACD,理由为:
证明:∵△ABC与△ADE都为等腰直角三角形,
∴AB=AC,AD=AE,且∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠DAE+∠EAC,即∠BAE=∠CAD,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ACD(SAS);
(2)答:△ADF∽△CEF,理由为:
证明:∵△ABE≌△ACD,
∴∠ADC=∠AEB,
∵∠AFD=∠EFC,
∴△ADF∽△CEF.
点评 此题考查了相似三角形的判定与性质,以及全等三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.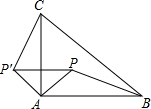 如图,△ABC中,∠BAC=90°,AC=AB,P是△ABC內一点,PA=1,连PB,把△ABP绕点A逆时针旋转90°后,点P的对应点为P′,则点P与点P′之间的距离为( )
如图,△ABC中,∠BAC=90°,AC=AB,P是△ABC內一点,PA=1,连PB,把△ABP绕点A逆时针旋转90°后,点P的对应点为P′,则点P与点P′之间的距离为( )
 如图,△ABC中,∠BAC=90°,AC=AB,P是△ABC內一点,PA=1,连PB,把△ABP绕点A逆时针旋转90°后,点P的对应点为P′,则点P与点P′之间的距离为( )
如图,△ABC中,∠BAC=90°,AC=AB,P是△ABC內一点,PA=1,连PB,把△ABP绕点A逆时针旋转90°后,点P的对应点为P′,则点P与点P′之间的距离为( )| A. | A$\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
12.下列四幅汽车标志,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图所示,在△ABC中,∠A=90°,BD平分∠ABC,AD=2cm,AB+BC=8,S△ABC=8cm2.
如图所示,在△ABC中,∠A=90°,BD平分∠ABC,AD=2cm,AB+BC=8,S△ABC=8cm2.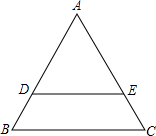 如图,已知△ABC是等边三角形,D、E分别是AB、AC边上的点,且DB=EC.
如图,已知△ABC是等边三角形,D、E分别是AB、AC边上的点,且DB=EC.