题目内容
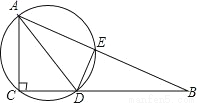
如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC，过A，C，D三点的圆与斜边AB交于点E，连接DE．
（1）求证：AC=AE；
（2）若AC=6，CB=8，求△ACD外接圆的直径．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
期末100分闯关海淀考王系列答案小学能力测试卷系列答案题目内容
如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC，过A，C，D三点的圆与斜边AB交于点E，连接DE．
（1）求证：AC=AE；
（2）若AC=6，CB=8，求△ACD外接圆的直径．
期末100分闯关海淀考王系列答案小学能力测试卷系列答案
，对角线
，点E是边AB的中点，CE与BD相交于点
.
求证：BD平分
；
求证： 
．
=
，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．
．
∴
B. ∵
∴
∴
D. ∵
，∴