题目内容
11.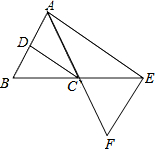 如图,已知△ABC中,CD为∠ACB的平分线,AE∥CD交BC的延长线于E,EF⊥AE交AC的延长线于F.
如图,已知△ABC中,CD为∠ACB的平分线,AE∥CD交BC的延长线于E,EF⊥AE交AC的延长线于F.(1)求证:AC=CE;
(2)若AC=5,求AF.
分析 (1)根据CD为∠ACB的平分线,得到∠BCD=∠ACD,又AE∥CD,所以∠ACD=∠EAC,∠BCD=∠AEC,从而∠EAC=∠AEC,即可解答;
(2)利用EF⊥AE,得到∠FEC=∠F,进而得到EC=CF,根据AC=CE,从而得到AC=CE=CF,即可解答.
解答 解:(1)∵CD为∠ACB的平分线,
∴∠BCD=∠ACD,
∵AE∥CD,
∴∠ACD=∠EAC,∠BCD=∠AEC,
∴∠EAC=∠AEC,
∴AC=CE.
(2)∵EF⊥AE,
∴∠AEC+∠FEC=90°,∠EAC+∠F=90°,
∵∠AEC=∠EAC,
∴∠FEC=∠F,
∴EC=CF,
∵AC=CE,
∴AC=CE=CF,
∴AF=2AC=10.
点评 本题考查了平行线的性质、等角对等边,解决本题的关键是由相等的角得到相等的边.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
19.下列各点中,在第四象限的点是( )
| A. | (1,3) | B. | (1,-3) | C. | (-1,-3) | D. | (-1,3) |
20. 如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )
 如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
1. 如图,∠1=∠2,∠C=130°,∠2=22°,则∠DAC的度数是( )
如图,∠1=∠2,∠C=130°,∠2=22°,则∠DAC的度数是( )
 如图,∠1=∠2,∠C=130°,∠2=22°,则∠DAC的度数是( )
如图,∠1=∠2,∠C=130°,∠2=22°,则∠DAC的度数是( )| A. | 25° | B. | 24° | C. | 28° | D. | 22° |




 若正比例函数y=kx的图象如图所示,则一次函数y=x+k的图象大致是( )
若正比例函数y=kx的图象如图所示,则一次函数y=x+k的图象大致是( )



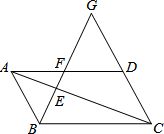 如图,在平行四边形ABCD中,点E是对角线AC上一点,且EC=2AE,连接BE并延长交AD于点F,交CD延长线于点G,则$\frac{BE}{EG}$=$\frac{1}{2}$.
如图,在平行四边形ABCD中,点E是对角线AC上一点,且EC=2AE,连接BE并延长交AD于点F,交CD延长线于点G,则$\frac{BE}{EG}$=$\frac{1}{2}$.