题目内容
 (1)点(1,3)沿X轴的正方向平移4个单位得到的点的坐标是______;
(1)点(1,3)沿X轴的正方向平移4个单位得到的点的坐标是______;
(2)直线y=3x沿x轴的正方向平移4个单位得到的直线解析式为______;
(3)若直线l与(2)中所得的直线关于直线x=2对称,试求直线l的解析式.
解:(1)横坐标=1+4=5,
∴平移后的坐标为:(5,3);
(2)平移后的解析式为:y=3(x-4)=3x-12.
(3)设直线l的解析式为:y=kx+b,
∵点(4,0)和(0,-12)在直线y=3x-12上,
它们关于直线x=2的对称点为:(0,0)(4,-12)
将x=0,y=0和x=4,y=-12分别代入y=kx+b中,得:
解得:
∴直线l的解析式为:y=-3x.
故答案为:(5,3);y=3x-12.
分析:(1)沿x轴平移,纵坐标不变,横坐标加4即可得出平移后的坐标;
(2)根据左右平移时,纵坐标不变,横坐标左移加、右移减的法则进行求解即可;
(3)先找出(2)中所求解析式的两个点的坐标,然后求出这两个坐标关于x=2对称的点的坐标,然后利用待定系数法即可求出l的解析式.
点评:本题考查函数图象的平移规律及待定系数法的运用,解答此类题目的关键是掌握函数左右平移,纵坐标不变,横坐标左移加、右移减;函数上下平移,横坐标不变,纵坐标上移加、下移减.
∴平移后的坐标为:(5,3);
(2)平移后的解析式为:y=3(x-4)=3x-12.
(3)设直线l的解析式为:y=kx+b,
∵点(4,0)和(0,-12)在直线y=3x-12上,
它们关于直线x=2的对称点为:(0,0)(4,-12)
将x=0,y=0和x=4,y=-12分别代入y=kx+b中,得:

解得:

∴直线l的解析式为:y=-3x.
故答案为:(5,3);y=3x-12.
分析:(1)沿x轴平移,纵坐标不变,横坐标加4即可得出平移后的坐标;
(2)根据左右平移时,纵坐标不变,横坐标左移加、右移减的法则进行求解即可;
(3)先找出(2)中所求解析式的两个点的坐标,然后求出这两个坐标关于x=2对称的点的坐标,然后利用待定系数法即可求出l的解析式.
点评:本题考查函数图象的平移规律及待定系数法的运用,解答此类题目的关键是掌握函数左右平移,纵坐标不变,横坐标左移加、右移减;函数上下平移,横坐标不变,纵坐标上移加、下移减.

练习册系列答案
相关题目


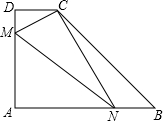 (2013•同安区一模)如图所示,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,tanB=1.动点M、N分别从点D、B同时出发,沿线段DA和BA向A方向运动,动点N的运动速度是动点M运动速度的两倍,当点M或点N谁先运动到点A时,M、N两点同时停止运动.设动点M的运动速度是1个单位/秒,M、N运动的时间为x秒.
(2013•同安区一模)如图所示,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,tanB=1.动点M、N分别从点D、B同时出发,沿线段DA和BA向A方向运动,动点N的运动速度是动点M运动速度的两倍,当点M或点N谁先运动到点A时,M、N两点同时停止运动.设动点M的运动速度是1个单位/秒,M、N运动的时间为x秒.
 如图,有一个圆柱体,它的高等于12cm,底面半径等于3cm,一只蚂蚁在点A处,它要吃到上底面上与A点相对的点B处的食物,沿圆柱体侧面爬行的最短路程是
如图,有一个圆柱体,它的高等于12cm,底面半径等于3cm,一只蚂蚁在点A处,它要吃到上底面上与A点相对的点B处的食物,沿圆柱体侧面爬行的最短路程是