题目内容
 如图,已知OA=OB=OC,且∠AOB=k∠BOC,则∠ACB是∠BAC的
如图,已知OA=OB=OC,且∠AOB=k∠BOC,则∠ACB是∠BAC的
- A.
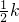 倍
倍 - B.k倍
- C.2k
- D.

B
分析:由OA=OB=OC,得到A,B,C在以O为圆心的同一个圆上,则∠AOB=2∠ACB,∠BOC=2∠BAC,而∠AOB=k∠BOC,即可得到∠ACB=k∠BAC.
解答: 解:∵OA=OB=OC,
解:∵OA=OB=OC,
∴A,B,C在以O为圆心的同一个圆上,如图,
∴∠AOB=2∠ACB,∠BOC=2∠BAC,
而∠AOB=k∠BOC,
即2∠ACB=k•2∠BAC,
∴∠ACB=k∠BAC.
故选B.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.同时考查了圆周角定理.
分析:由OA=OB=OC,得到A,B,C在以O为圆心的同一个圆上,则∠AOB=2∠ACB,∠BOC=2∠BAC,而∠AOB=k∠BOC,即可得到∠ACB=k∠BAC.
解答:
 解:∵OA=OB=OC,
解:∵OA=OB=OC,∴A,B,C在以O为圆心的同一个圆上,如图,
∴∠AOB=2∠ACB,∠BOC=2∠BAC,
而∠AOB=k∠BOC,
即2∠ACB=k•2∠BAC,
∴∠ACB=k∠BAC.
故选B.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.同时考查了圆周角定理.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目

 17、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有( )
17、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有( ) 长线交于点E.
长线交于点E. 如图,已知OA=OB,那么数轴上点A与点C的距离是
如图,已知OA=OB,那么数轴上点A与点C的距离是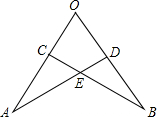 如图,已知OA=OB,OC=OD,下列结论中(1)∠A=∠B;(2)DE=CE;(3)连OE,OE平分∠O,正确的有
如图,已知OA=OB,OC=OD,下列结论中(1)∠A=∠B;(2)DE=CE;(3)连OE,OE平分∠O,正确的有