Question

【题目】春节即将来临，某企业接到一批礼品生产任务，约定这批礼品的出厂价为每件6元，按要求在20天内完成．为了按时完成任务，该企业招收了新工人，设新工人小王第x天生产的礼品数量为y件，y与x满足如下关系：y＝.

（1）小王第几天生产的礼品数量为390件？

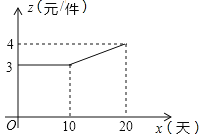
（2）如图，设第x天生产的每件礼品的成本是z元，z与x之间的关系可用图中的函数图象来刻画．若小王第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润＝出厂价﹣成本）

Answer 1

【答案】（1）第12天生产的礼品数量为390只；（2）w与x的函数表达式为w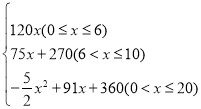＝，第18天利润最大，最大利润为1188元．

【解析】

（1）因为前6天最多可生产礼品240只，所以把y=390代入y=25x+90，解方程即可求得；

（2）先根据图象求得成本z与x之间的关系，然后根据利润等于出厂价减去成本价，分0≤x≤6，6＜x≤10，10＜x≤20三种情况讨论，再根据一次函数的增减性和二次函数的增减性解答．

（1）∵6×40＝240，

∴前六天中第6天生产的礼品最多达到240只，

将390代入y=25x+90得：25x+90＝390，

∴x＝12，

答：第12天生产的礼品数量为390只；

（2）当0≤x＜10时，z＝3，

当10≤x≤20时，设z＝kx+b，将（10，3）和（20，4）代入，

得

解得：，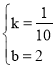

∴z＝x+2；

当0≤x≤6时，w＝（6﹣3）×40x＝120x，w随x的增大而增大，

∴当x＝6时最大值为720元；

当6＜x≤10时，w＝（6﹣3）×（25x+90）＝75x+270，w随x的增大而增大，

∴当x＝10时最大值为1020元；

当10＜x≤20时，w＝（6﹣x﹣2）（25x+90）＝﹣x2+91x+360，

∵对称轴为：直线x＝18，天数为整数，

∴将x＝18代入得w＝1188元；

综上所述，w与x的函数表达式为w＝，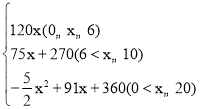

答：第18天利润最大，最大利润为1188元．