Question

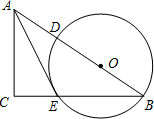如图，∠C=90°，∠CAE=∠ABC，AC=2，BC=3．
（1）判断AE与⊙O的位置关系，并说明理由；
（2）求OB的长．

Answer 1

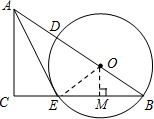（1）证明：连接OE，
∵OE=OB，
∴∠OEB=∠OBE，
又∵∠CAE=∠ABC，
∴∠OEB=∠ABC=∠CAE，
∴∠AEC+∠OEB=90°，
∴∠AEO=90°，
∴AE与⊙O相切．

（2）解：过点O作OM⊥BE，于点M，
∵∠C=∠C=90°，∠CAE=∠ABC，
∴△ACE∽△BCA，
∴=，
∴，，
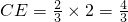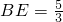则BM=，
AB==，
∵∠C=90°，∠OMB=90°，
∴OM∥AC，
∴△BOM∽△BAC，
∴=，
∴，
∴．
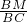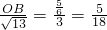分析：（1）根据等腰三角形的性质以及∠CAE=∠ABC得出∠OEB=∠ABC=∠CAE，进而得出∠AEC+∠OEB=90°，求出答案即可；
（2）根据相似三角形的判定得出△ACE∽△BCA，进而得出AB，BM的长，再利用△BOM∽△BAC，得出=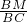求出BO即可．
点评：此题主要考查了切线的判定以及相似三角形的判定与性质，根据已知作出辅助线OM⊥BE进而求出BM的长是解题关键．