题目内容
已知四个三角形分别满足下列条件:①三角形的三边之比为 1:1: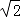 ;②三角形的三边分别 是 9、40、41;③三角形三内角之比为 1:2:3;④三角形一边上的中线等于这边的一半.其中直 角三角形有( )个.
;②三角形的三边分别 是 9、40、41;③三角形三内角之比为 1:2:3;④三角形一边上的中线等于这边的一半.其中直 角三角形有( )个.
A.4 B.3 C.2 D.1
A考点】勾股定理的逆定理.
【分析】根据勾股定理的逆定理或三角形的内角和定理即可进行判断,从而得到答案.
【解答】解:①因为 12+12=(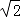 )2 三边符合勾股定理的逆定理,故是直角三角形;
)2 三边符合勾股定理的逆定理,故是直角三角形;
②因为 92+402=412 三边符合勾股定理的逆定理,故是直角三角形;
③设最小的角为 x,则 x+2x+3x=180°,则三角分别为 30°,60°,90°,故是直角三角形;
④因为符合直角三角形的判定,故是直角三角形. 所以有 4 个直角三角形.
故选:A.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长, 只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
相关题目
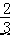 )×
)× 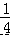 ﹣|﹣4|3÷(﹣2)4
﹣|﹣4|3÷(﹣2)4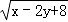 =0,则 yx 的值是( )
=0,则 yx 的值是( ) A.
A. 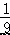 B.﹣6 C.9 D.﹣
B.﹣6 C.9 D.﹣