Question

【题目】（综合与实践

如图，直线的函数关系式为，且与轴交于点A，直线经过点B（2，0），C（－1，3），直线与交于点D．

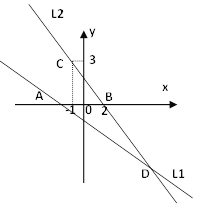
(1)求直线的函数关系式；

(2)求△ABD的面积．

(3)点P是轴上一动点，问是否存在一点P，恰好使△ADP为直角三角形？若存在，直接写出点P的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）y=－x+2；（2）8；（3）存在，点P的坐标为（6,0）或（8,0）

【解析】

（1）根据直线l2经过点A（2，0），B（-1，3），可以求得直线l2的函数关系式；
（2）将直线l1和直线l2的函数表达式联立成二元一次方程组，即可求得点D的坐标；根据直线l1的表达式可以求得点A的坐标，即可求得△ABD的面积．

（3）分∠APD=90°时、∠ADP=90°时两种情况讨论.

（1）设直线l2的函数关系式为：y=kx+b，

∵直线过点B（2，0），C（－1，3），

∴

解得：，

∴直线l2的函数关系式为：y=－x+2；

（2）过点D作DE⊥x轴，垂足为点E

∵直线l1与l2交于点D．

∴，解得，

∴ D（6，-4）

∴DE=4

将y=0代入y＝－x－1得x=－2，

∴点A的坐标是（－2，0），

∵点B的坐标是（2，0），

∴AB=4..

∴S△ABC＝AB×DE＝×4×4＝8．

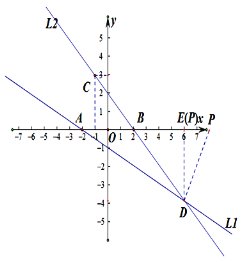
（3）存在一点P，恰好使△ADP为直角三角形， 点P的坐标为（6,0）或（8,0）. 理由是：

当∠APD=90°时，P1点坐标为（6,0）

当∠ADP=90°时，设P（x，0）

可列方程为：42＋（x－6）2＝（x＋2）2－（42＋82）

解得：x＝8

所以P(8,0)

∴点P的坐标为（6,0）或（8,0）