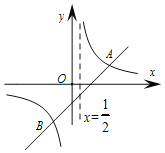
��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�![]() �Ķ�������ֱ�Ϊ
�Ķ�������ֱ�Ϊ![]() ��
��![]() ��
��![]() .����
.����![]() ��
��![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() ������
������![]() ��
��![]() ��
��![]() ������
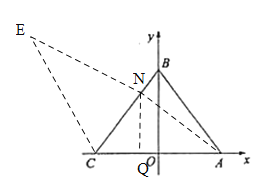
������![]() ������ÿ��1����λ���ȵ��ٶ��ƶ�����һ�����㵽���յ�
������ÿ��1����λ���ȵ��ٶ��ƶ�����һ�����㵽���յ�![]() ʱ����һ������Ҳ��ֹ֮ͣ�ƶ����ƶ�ʱ���Ϊ
ʱ����һ������Ҳ��ֹ֮ͣ�ƶ����ƶ�ʱ���Ϊ![]() �룬����
�룬����![]() .
.
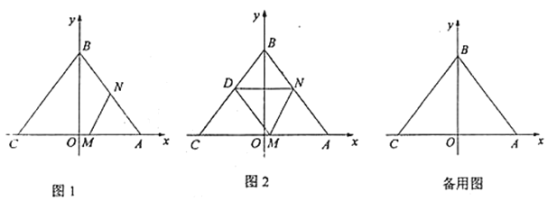
������ͼ1������![]() �ƶ���
�ƶ���![]() �е�ʱ�����ʱ
�е�ʱ�����ʱ![]() ��ֵ��
��ֵ��![]() �����ꣻ
�����ꣻ
�������ƶ������У���![]() ��ֱ��
��ֱ��![]() ���ۣ���
���ۣ���![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() .
.
����ͼ2������![]() ǡ������
ǡ������![]() ���ϵĵ�
���ϵĵ�![]() ��ʱ�����ʱ
��ʱ�����ʱ![]() ��ֵ��
��ֵ��
�ڵ���![]() �ƶ�����
�ƶ�����![]() ʱ����
ʱ����![]() ���ڵ�
���ڵ�![]() �������ʱ��
�������ʱ��![]() �����ֱ꣨��д��������ɣ�.
�����ֱ꣨��д��������ɣ�.
���𰸡�����![]() ,��
,��![]() ����Ϊ
����Ϊ![]() ; ����
; ����![]() ; ��
; ��![]() ������Ϊ
������Ϊ![]()
��������
(1)���ݵ�����꣬�����AB�ij�������N��AB���е㣬�ɵ�AN�ij��ȣ��Ӷ����t��������M�������;
(2)���ɷ��ŵ����ʿɵ��ı���![]() Ϊ���Σ�����
Ϊ���Σ�����![]() �ᣬ�ɵõ�
�ᣬ�ɵõ�![]() ����
����![]() ���Ӷ����t.
���Ӷ����t.
�ڸ������ƿ������N(![]() )����E(x,y),���ݹ��ɶ����г�������:EM=6,EN=5,��ü��������E.
)����E(x,y),���ݹ��ɶ����г�������:EM=6,EN=5,��ü��������E.
����![]() ��
��![]() ��
��
��![]() ��
��![]() ����
����![]() .
.
����![]() �ƶ���
�ƶ���![]() �е�ʱ��������ɵ�
�е�ʱ��������ɵ�![]() ��
��
��![]() .
.
��![]() ��
��
���![]() ����Ϊ
����Ϊ![]() .
.
����������ɵ�![]() ��
��
��![]() ��ֱ��
��ֱ��![]() ���ۣ���
���ۣ���![]() ���ڵ�
���ڵ�![]() ����
����
��![]() ��
��
���ı���![]() Ϊ���Σ�
����
��![]() ��
��![]() �ᣬ
�ᣬ
��![]() ��
��
��![]() ��
��![]() ��
��
���![]() .
.
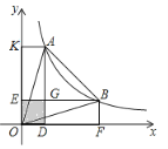
���ڹ�N��X��Ĵ��ߣ�����ΪQ������CNQ�ס�BCO��
�֡�BN=1,AC=6,BC=5,
��![]() ,��N(
,��N(![]() )��
)��
��E(x,y),��CE=6,EN=5,
��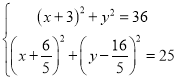
��ã�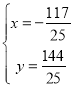
![]() ������Ϊ
������Ϊ![]() .
.