Question

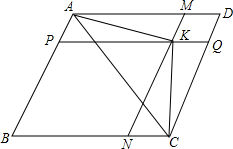如图，在?ABCD中，P、Q、M、N分别在AB、CD、AD、BC上，且MN∥AB，PQ∥BC，MN与PQ相交于K，
求证：2S_△ACK=S_?BNKP-S_?MKQD．

Answer 1

考点：平行四边形的性质

专题：证明题

分析：根据平行四边形的性质得到S_△ACK=

1

2

S_?ABCD，然后利用分割法来推知图中相关三角形、四边形间的数量关系．

解答：证明：如图，∵四边形ABCD是平行四边形，AC是对角线，
∴S_△ACK=

1

2

S_?ABCD，
在△ACD中，S_△ACK=S_△ACD-S_{四边形MKQD}-S_△AKM-S_△CKQ
=

1

2

S_?ABCD-S_{四边形MKQD}-

1

2

S_APKM-

1

2

S_CNKQ
∴2S_△ACK=S_ABCD-2S_MKQD-S_APKM-S_CNKQ
=（S_ABCD-S_MKQD-S_APKM-S_CNKQ）-S_MKQD
=S_BNKP-S_MKQD

点评：本题考查了平行四边形的性质．解题时，要注意数形结合数学思想的应用．