题目内容
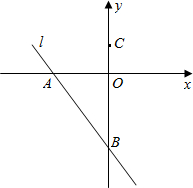 如图,直线y=
如图,直线y=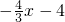 与x轴、y轴分别交于A、B两点.
与x轴、y轴分别交于A、B两点.
(1)求OA、OB的长;
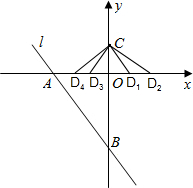
(2)已知点C(0,1),在x轴上是否存在点D,使得以D、C、O为顶点的三角形与△AOB相似?若存在,请直接写出D点的坐标;若不存在,请说明理由.
 解:(1)∵直线y=
解:(1)∵直线y=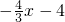 与x轴、y轴分别交于A、B两点,
与x轴、y轴分别交于A、B两点,∴当x=0,y=-4,当y=0,x=-3,
∴A点坐标为:(-3,0),B点坐标为:(0,-4);
∴OA=3,OB=4;
(2)当△D1OC∽△AOB,
则
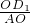 =
=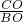 ,
,∵点C(0,1),∴CO=1,
∵OA=3,OB=4;
∴
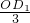 =
= ,
,解得:OD1=
 ,
,故D点坐标为:(
 ,0),
,0),当△COD2∽△AOB,
则
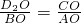 ,
,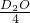 =
= ,
,解得:D2O=
 ,
,故D点坐标为:(
 ,0),
,0),根据当D点在x轴负半轴时,D点坐标为:(-
 ,0),(-
,0),(- ,0),也可以使得以D、C、O为顶点的三角形与△AOB相似,
,0),也可以使得以D、C、O为顶点的三角形与△AOB相似,综上所述:
使得以D、C、O为顶点的三角形与△AOB相似的D点坐标为:(-
 ,0),(-
,0),(- ,0),(
,0),( ,0),(
,0),( ,0).
,0).分析:(1)根据直线y=
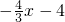 与x轴、y轴分别交于A、B两点,利用图象与坐标轴交点求法分别得出即可;
与x轴、y轴分别交于A、B两点,利用图象与坐标轴交点求法分别得出即可;(2)根据相似三角形的判定,以及AO,BO,CO的长度,得出对应边关系求出即可.
点评:此题主要考查了相似三角形的判定与性质以及一次函数与坐标轴交点坐标求法,根据D、C、O为顶点的三角形与△AOB对应顶点不确定,分别讨论得出是解题关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
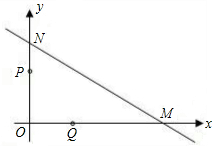
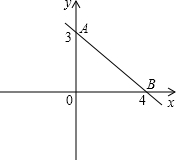 如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).
如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).

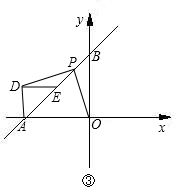
 点同时停止运动,设运动时间为t秒.
点同时停止运动,设运动时间为t秒. 已知:如图,直线AB与x轴交于点A,与y轴交于点B.
已知:如图,直线AB与x轴交于点A,与y轴交于点B.