题目内容
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m) 
【答案】解:延长CD交AH于点E,如图所示:根据题意得:CE⊥AH,
设DE=xm,则CE=(x+2)m,
在Rt△AEC和Rt△BED中,tan37°= ![]() ,tan60°=
,tan60°= ![]() ,
,
∴AE= ![]() ,BE=
,BE= ![]() ,
,
∵AE﹣BE=AB,
∴ ![]() ﹣
﹣ ![]() =10,
=10,
即 ![]() ﹣
﹣ ![]() =10,
=10,
解得:x≈5.8,
∴DE=5.8m,
∴GH=CE=CD+DE=2m+5.8m=7.8m.
答:GH的长为7.8m.
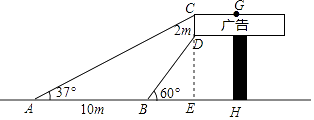
【解析】首先构造直角三角形,设DE=xm,则CE=(x+2)m,由三角函数得出AE和BE,由AE=BE=AB得出方程,解方程求出DE,即可得出GH的长.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目