题目内容
(2011•翔安区质检)(1)计算:(
)-1×(π-
)0-
+(-1)2
(2)计算:2
×(3
-4
)
(3)解方程:x2+5x+2=0.
| 1 |
| 3 |
| 2 |
| 9 |
(2)计算:2
| 12 |
| 8 |
|
(3)解方程:x2+5x+2=0.
分析:(1)根据零指数幂和负整数指数幂的意义得到原式=3×1-3+1,再进行实数运算;
(2)先把各二次根式化为最简二次根式得到原式=4
×(6
-4×
),再计算括号内的运算,最后进行二次根式的乘法运算;
(3)先计算出b2-4ac=25-8=17,然后代入一元二次方程的求根公式即可.
(2)先把各二次根式化为最简二次根式得到原式=4
| 3 |
| 2 |
| ||
| 2 |
(3)先计算出b2-4ac=25-8=17,然后代入一元二次方程的求根公式即可.
解答:(1)解:原式=3×1-3+1
=1;
(2)解:原式=4
×(6
-4×
)
=4
×(6
-2
)
=4
×4
=16
;
(3)解:∵a=1,b=5,c=2,
∴b2-4ac=25-8=17,
∴x=
,
∴x1=
,x2=
.
=1;
(2)解:原式=4
| 3 |
| 2 |
| ||
| 2 |
=4
| 3 |
| 2 |
| 2 |
=4
| 3 |
| 2 |
=16
| 6 |
(3)解:∵a=1,b=5,c=2,
∴b2-4ac=25-8=17,
∴x=
-5±
| ||
| 2 |
∴x1=
-5+
| ||
| 2 |
-5-
| ||
| 2 |
点评:本题考查了解一元二次方程-公式法:一元二次方程ax2+bx+c=0(a≠0)的求根公式为x=
(b2-4ac≥0).也考查了零指数幂、负整数指数幂以及二次根式的混合运算.
-b±
| ||
| 2a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
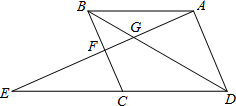 (2011•翔安区质检)如图,点E为平行四边形ABCD中DC边的延长线上的点,且CE=DC,连接AE,分别交BC、BD于点F、G.
(2011•翔安区质检)如图,点E为平行四边形ABCD中DC边的延长线上的点,且CE=DC,连接AE,分别交BC、BD于点F、G.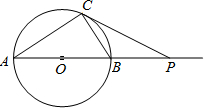 (2011•翔安区质检)如图,⊙0的直径AB=6cm,P是AB延长线上的一点,过点P作⊙0的切线,切点为C,连接AC,BC.
(2011•翔安区质检)如图,⊙0的直径AB=6cm,P是AB延长线上的一点,过点P作⊙0的切线,切点为C,连接AC,BC.