题目内容
14.已知一次函数的图象过A(-3,-5),B(1,3)两点.(1)求这个一次函数的表达式;
(2)试判断点P(-2,1)是否在这个一次函数的图象上.
分析 (1)设一次函数解析式为y=kx+b,将A(-3,-5),B(1,3)代入解得k、b可得解析式;
(2)将x=-2代入一次函数解析式可判断结果.
解答 解:(1)设一次函数解析式为y=kx+b,
将A(-3,-5),B(1,3)代入得,
$\left\{\begin{array}{l}{-5=-3k+b}\\{\;}\\{3=k+b}\end{array}\right.$,
解得,
$\left\{\begin{array}{l}{k=2}\\{\;}\\{b=1}\end{array}\right.$,
∴一次函数解析式为:y=2x+1;
(2)把x=-2代入y=2x+1,解得y=-3,
∴点P(-2,1)不在一次函数图象上.
点评 本题主要考查对一次函数的图象上点的坐标特征,解二元一次方程组,用待定系数法求出一次函数的解析式等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键.

练习册系列答案
相关题目
6.化简$\sqrt{8{a}^{2}}$的结果是( )
| A. | 4a$\sqrt{2}$ | B. | 16$\sqrt{{a}^{2}}$ | C. | 2a$\sqrt{4}$ | D. | 2a$\sqrt{2}$ |
 如图,∠3和∠9是直线AD、BD被直线AC所截而成的同位角;∠6和∠9是直线BC、AC被直线BD所截而成的同位角.
如图,∠3和∠9是直线AD、BD被直线AC所截而成的同位角;∠6和∠9是直线BC、AC被直线BD所截而成的同位角.
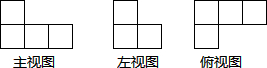 在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画出来,如图,则这堆货箱共有5个.
在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画出来,如图,则这堆货箱共有5个.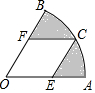 如图,在扇形OAB中,∠O=60°,OA=4$\sqrt{3}$,四边形OECF是扇形OAB中最大的菱形,其中点E,C,F分别在OA,$\widehat{AB}$,OB上,则图中阴影部分的面积为8π-8$\sqrt{3}$.
如图,在扇形OAB中,∠O=60°,OA=4$\sqrt{3}$,四边形OECF是扇形OAB中最大的菱形,其中点E,C,F分别在OA,$\widehat{AB}$,OB上,则图中阴影部分的面积为8π-8$\sqrt{3}$.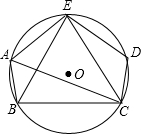 如图,△ABC是⊙O的内接三角形,点D,E在⊙O上,连接AE,DE,CD,BE,CE,∠EAC+∠BAE=180°,$\widehat{AB}$=$\widehat{CD}$.
如图,△ABC是⊙O的内接三角形,点D,E在⊙O上,连接AE,DE,CD,BE,CE,∠EAC+∠BAE=180°,$\widehat{AB}$=$\widehat{CD}$.