Question

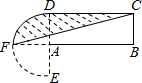（1998•南京）设计一个商标图象（如图阴影部分），矩形ABCD中，AB=2BC，且AB=8cm，以点A为圆心，AD的长为半径作半圆，则商标图案面积等于（　　）

A．4π+8

B．4π+16

C．3π+8

D．3π+16

Answer 1

分析：根据矩形的性质得到AD=BC=4，∠FAD=90°，根据图形得到S_阴=S_矩ABCD+S_扇ADF-S_△FBC．

解答：解：∵矩形ABCD中，AB=2BC，且AB=8cm，
∴AD=BC=4，
∴S_阴=S_矩ABCD+S_扇ADF-S_△FBC，
∵S_矩ABCD=AB•BC=8×4=32，
S_扇ADF=

90π×42

360

=4π，
S_△FBC=

1

2

BC•FB=

1

2

×4×（8+4）=24，
∴S_阴=32+4π-24=（8+4π）cm²．
所以商标图案的面积为（8+4π）cm²．
故选A．

点评：本题考查了扇形的面积公式：S=

nπr2

360

（其中n为扇形的圆心角的度数，r为半径）．也考查了矩形的性质．