题目内容
我国计划在 2020 年左右发射火星探测卫星.据科学研究,火星距离地球的最近距离约为 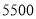 万千米,这个数据用科学计数法可表示为
万千米,这个数据用科学计数法可表示为 
A. 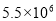 千 B.
千 B. 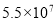 千米 C.
千米 C. 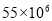 千米 D.
千米 D. 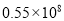 千米
千米
练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
题目内容
我国计划在 2020 年左右发射火星探测卫星.据科学研究,火星距离地球的最近距离约为 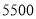 万千米,这个数据用科学计数法可表示为
万千米,这个数据用科学计数法可表示为 
A. 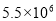 千 B.
千 B. 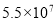 千米 C.
千米 C. 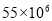 千米 D.
千米 D. 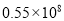 千米
千米
 名题金卷系列答案
名题金卷系列答案