题目内容
在一次航空模型的设计制作中,需将两个半径为12cm和4cm的圆木棍用铁丝紧紧扎在一起,则最少需铁丝________cm(接头忽略不计).
(16 +
+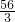 π)
π)
分析:如图,根据题意可以知道所求的铁丝长度为2AB+ +
+ ,而
,而 的度数为120°,接着利用弧长公式和相切两圆的性质即可求解.
的度数为120°,接着利用弧长公式和相切两圆的性质即可求解.
解答: 解:如图,∵被铁丝捆绑在一起的两根底面半径为12cm、4cm的圆外切,
解:如图,∵被铁丝捆绑在一起的两根底面半径为12cm、4cm的圆外切,
设AB,CD与两圆分别相切于点A,B,C,D,
∴CD=AB,
过点O′作O′E⊥BO于点E,
∴EO=12-4=8cm,OO′=16cm,
∴EO′= =8
=8 cm,
cm,
∴AB=CD=8 cm,
cm,
∴sin∠EO′O= =
= ,
,
∴∠EO′O=30°,
∴∠BOO′=60°,
∴∠BOD=120°,
∴ =
= =16π,
=16π,
 =
=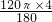 =
= π,
π,
∴所求铁丝长度为:8 +8
+8 +16π+
+16π+ π=16
π=16 +
+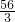 π,
π,
∴所求铁丝的长度(16 +
+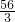 π)cm.
π)cm.
故答案为:16 +
+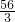 π.
π.
点评:此题主要考查了相切两圆的性质,解题时首先正确理解题意,然后根据题意得到所求的铁丝长度,最后利用弧长公式和相切两圆的性质即可求解.
 +
+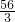 π)
π)分析:如图,根据题意可以知道所求的铁丝长度为2AB+
 +
+ ,而
,而 的度数为120°,接着利用弧长公式和相切两圆的性质即可求解.
的度数为120°,接着利用弧长公式和相切两圆的性质即可求解.解答:
 解:如图,∵被铁丝捆绑在一起的两根底面半径为12cm、4cm的圆外切,
解:如图,∵被铁丝捆绑在一起的两根底面半径为12cm、4cm的圆外切,设AB,CD与两圆分别相切于点A,B,C,D,
∴CD=AB,
过点O′作O′E⊥BO于点E,
∴EO=12-4=8cm,OO′=16cm,
∴EO′=
 =8
=8 cm,
cm,∴AB=CD=8
 cm,
cm,∴sin∠EO′O=
 =
= ,
,∴∠EO′O=30°,
∴∠BOO′=60°,
∴∠BOD=120°,
∴
 =
= =16π,
=16π, =
=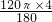 =
= π,
π,∴所求铁丝长度为:8
 +8
+8 +16π+
+16π+ π=16
π=16 +
+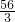 π,
π,∴所求铁丝的长度(16
 +
+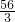 π)cm.
π)cm.故答案为:16
 +
+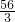 π.
π.点评:此题主要考查了相切两圆的性质,解题时首先正确理解题意,然后根据题意得到所求的铁丝长度,最后利用弧长公式和相切两圆的性质即可求解.

练习册系列答案
相关题目