题目内容
 已知抛物线
已知抛物线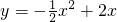 与直线y=kx都经过原点和点E
与直线y=kx都经过原点和点E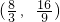 .
.
(1)k=______;
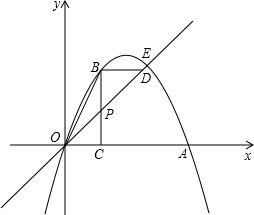
(2)如图,点P是直线y=kx(x>0)上的一个动点,过点P作x轴的垂线,垂足是点C,交抛物线于点B,过点B作x轴的平行线交直线y=kx于点D,连接OB;若以B、P、D为顶点的三角形与△OBC相似,则点P的坐标是______.
解:(1)∵直线y=kx经过点E( ,
, ),
),
∴ k=
k= ,
,
解得k= ;
;
(2)由(1)可知直线解析式为y= x,
x,
设点P的横坐标为x,则点P(x, x),B(x,-
x),B(x,- x2+2x),
x2+2x),
∵BD∥x轴,
∴∠BDP=∠POC,
∴tan∠BDP=tan∠POC= ,
,
即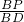 =
= ,
,
又∠DBP=∠BCO=90°,
①当∠BDP=∠BOC时,两三角形相似,
所以,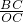 =
=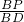 ,
,
即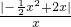 =
= ,
,
整理得,|x-4|= ,
,
所以,x-4= 或x-4=-
或x-4=- ,
,
解得x= 或x=
或x= ,
,
当x= 时,y=
时,y= x=
x= ×
× =
= ,
,
当x= 时,y=
时,y= x=
x= ×
× =
= ,此时点B、P重合,△BPD不存在,
,此时点B、P重合,△BPD不存在,
所以,点P( ,
, );
);
②∠BDP与∠BOC互余时,∠BDP=∠OBC,两三角形相似,
cot∠BOC=tan∠BDP= ,
,
所以,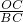 =
=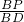 ,
,
即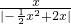 =
= ,
,
整理得,|x-4|=3,
所以,x-4=3或x-4=-3,
解得x=7或x=1,
当x=7时,y= x=
x= ×7=
×7= ,
,
当x=1时,y= x=
x= ×1=
×1= ,
,
所以,点P(7, )或(1,
)或(1, ),
),
综上所述,点P的坐标是( ,
, )或(7,
)或(7, )或(1,
)或(1, ).
).
故答案为:(1) ;(2)(
;(2)( ,
, )或(7,
)或(7, )或(1,
)或(1, ).
).
分析:(1)把点E的坐标代入直线解析式,计算即可求出k值;
(2)设点P的横坐标为x,根据直线解析式表示出点P,根据抛物线解析式表示出点B,根据两直线平行,内错角相等可得∠BDP=∠POC,然后根据∠BDP的正切值求出BP与BD的比值,根据点B的坐标求出∠BOC的正切值,再分①当∠BDP=∠BOC时,两三角形相似,②∠BDP与∠BOC互余时,∠BDP=∠OBC,两三角形相似,两三角形相似,再根据相似三角形对应边成比例列出比例式求解即可.
点评:本题是对二次函数的综合考查,主要涉及待定系数法求一次函数解析式,相似三角形对应边成比例,(2)要注意分情况讨论求解.
 ,
, ),
),∴
 k=
k= ,
,解得k=
 ;
;(2)由(1)可知直线解析式为y=
 x,
x,设点P的横坐标为x,则点P(x,
 x),B(x,-
x),B(x,- x2+2x),
x2+2x),∵BD∥x轴,
∴∠BDP=∠POC,
∴tan∠BDP=tan∠POC=
 ,
,即
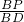 =
= ,
,又∠DBP=∠BCO=90°,
①当∠BDP=∠BOC时,两三角形相似,
所以,
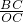 =
=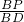 ,
,即
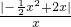 =
= ,
,整理得,|x-4|=
 ,
,所以,x-4=
 或x-4=-
或x-4=- ,
,解得x=
 或x=
或x= ,
,当x=
 时,y=
时,y= x=
x= ×
× =
= ,
,当x=
 时,y=
时,y= x=
x= ×
× =
= ,此时点B、P重合,△BPD不存在,
,此时点B、P重合,△BPD不存在,所以,点P(
 ,
, );
);②∠BDP与∠BOC互余时,∠BDP=∠OBC,两三角形相似,
cot∠BOC=tan∠BDP=
 ,
,所以,
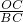 =
=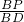 ,
,即
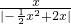 =
= ,
,整理得,|x-4|=3,
所以,x-4=3或x-4=-3,
解得x=7或x=1,
当x=7时,y=
 x=
x= ×7=
×7= ,
,当x=1时,y=
 x=
x= ×1=
×1= ,
,所以,点P(7,
 )或(1,
)或(1, ),
),综上所述,点P的坐标是(
 ,
, )或(7,
)或(7, )或(1,
)或(1, ).
).故答案为:(1)
 ;(2)(
;(2)( ,
, )或(7,
)或(7, )或(1,
)或(1, ).
).分析:(1)把点E的坐标代入直线解析式,计算即可求出k值;
(2)设点P的横坐标为x,根据直线解析式表示出点P,根据抛物线解析式表示出点B,根据两直线平行,内错角相等可得∠BDP=∠POC,然后根据∠BDP的正切值求出BP与BD的比值,根据点B的坐标求出∠BOC的正切值,再分①当∠BDP=∠BOC时,两三角形相似,②∠BDP与∠BOC互余时,∠BDP=∠OBC,两三角形相似,两三角形相似,再根据相似三角形对应边成比例列出比例式求解即可.
点评:本题是对二次函数的综合考查,主要涉及待定系数法求一次函数解析式,相似三角形对应边成比例,(2)要注意分情况讨论求解.

练习册系列答案
相关题目
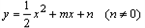 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴。
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴。
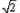 ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值。
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值。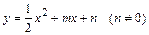 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴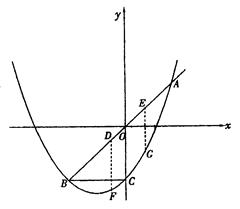
 ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.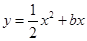 与直线
与直线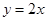 交于点
交于点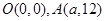 .点
.点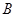 是抛物线上
是抛物线上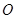 ,
,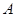 之间的一个动点,过点
之间的一个动点,过点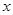 轴、
轴、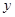 轴的平行线与直线
轴的平行线与直线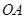 交于点
交于点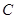 ,
,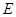 .
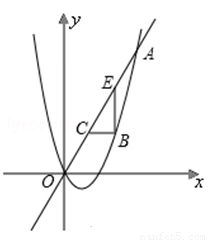
.
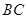 的长;
的长;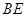 为边构造矩形
为边构造矩形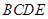 ,设点
,设点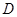 的坐标为
的坐标为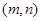 ,求出
,求出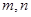 之间的关系式.
之间的关系式.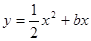 与直线
与直线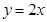 交于点O(0,0),A(
交于点O(0,0),A(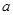 ,12),点B是抛物线上O,A之间的一个动点,过点B分别作
,12),点B是抛物线上O,A之间的一个动点,过点B分别作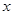 轴、
轴、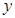 轴的平行线与直线OA交于点C,E.
轴的平行线与直线OA交于点C,E.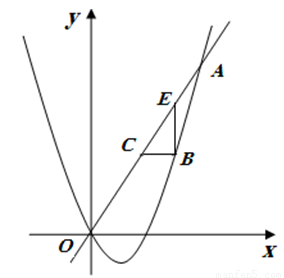
 ,
, ),求出
),求出