题目内容
如图，已知抛物线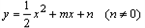
与直线y=x交于A、B两点，与y轴交于点C，OA＝OB，BC∥x轴。
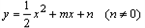与直线y=x交于A、B两点，与y轴交于点C，OA＝OB，BC∥x轴。
（1）求抛物线的解析式。
（2）设D、E是线段AB上异于A、B的两个动点（点E在点D的上方），DE＝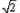
，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值。
（2）设D、E是线段AB上异于A、B的两个动点（点E在点D的上方），DE＝
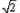，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值。解：（1）∵抛物线
与y轴交于点C，
∴C（0，n）
∵BC∥x轴
∴B点的纵坐标为n，
∵B、A在y=x上，且OA=OB
∴B（n，n），A（-n，-n），
∴
解得n=0（舍去），n=-2；m=1，
∴所求解析式为：
；
（2）作DH⊥EG于H，
∵D、E在直线y=x上，
∴∠EDH=45°，
∴DH=EH，
∵DE=
，
∴DH=EH=1，
∵D（x，x）
∴E（x+1，x+1），
∴F的纵坐标：
，G的纵坐标：
，
∴DF=x-（
）=2-
，EG=（x+1）- [
]=2-
，∴
，
，
，
∴x的取值范围是-2＜x＜1
当x=-
时，y最大值=3
。
与y轴交于点C，∴C（0，n）
∵BC∥x轴
∴B点的纵坐标为n，
∵B、A在y=x上，且OA=OB
∴B（n，n），A（-n，-n），
∴
解得n=0（舍去），n=-2；m=1，∴所求解析式为：
；（2）作DH⊥EG于H，
∵D、E在直线y=x上，
∴∠EDH=45°，
∴DH=EH，
∵DE=
，∴DH=EH=1，
∵D（x，x）
∴E（x+1，x+1），
∴F的纵坐标：
，G的纵坐标：，∴DF=x-（
）=2-，EG=（x+1）- []=2-，∴，，，∴x的取值范围是-2＜x＜1
当x=-
时，y最大值=3。
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
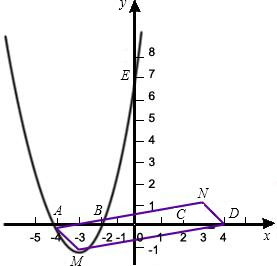如图，已知抛物线C1与坐标轴的交点依次是A（-4，0），B（-2，0），E（0，8）．
与坐标轴的交点依次是
，
，
．
的解析式；
，抛物线
轴分别交于
两点（点
在点
的左侧），顶点为
，四边形
的面积为
．若点
，点
，点
的面积
之间的关系式，并写出自变量
与坐标轴的交点依次是A(－4，0)，B(－2，0)，E(0，8)．
关于原点对称的抛物线
的解析式；
与x轴分别交于C、D两点(点C在点D的左侧)，顶点为N，四边形MDNA的面积为S．若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动；与此同时，点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动，直到点A与点D重合为止．求出四边形MDNA的面积S与运动时间t之间的关系式，并写出自变量t的取值范围；
