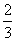题目内容
如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论: ①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )

A.1 B.2 C.3 D.4
D
【解析】①利用等边对等角,即可证得∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此可以求解;②证明∠POC=60°,且OP=OC,即可证得△OPC是等边三角形;③首先证明,△POA≌△CPE,则AO=CE,AC=AE+CE=AO+AP;④过带你C做CH⊥AB于H,根据S四边形AOCP=S△ACP+S△AOC,利用三角形的面积公式即可求解.所以4个结论都正确.
故选D.

练习册系列答案
相关题目
 ,则此扇形的弧长为 .
,则此扇形的弧长为 . C=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
C=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.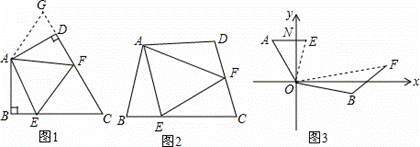
 ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;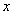 米,那么下列方程正确的是( )
米,那么下列方程正确的是( ) B.
B.
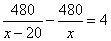 D.
D.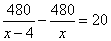

 )2+(tan45°)–1
)2+(tan45°)–1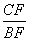 的值为( )
的值为( ) 
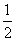 B.
B.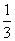 C.
C. D.
D.