Question

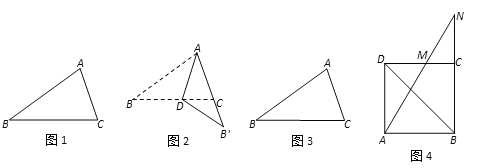
【题目】阅读材料：等腰三角形具有性质“等边对等角”．事实上，不等边三角形也具有类似性质“大边对大角”：如图1．在△ABC中，如果AB＞AC，那么∠ACB＞∠ABC．证明如下：将AB沿△ABC的角平分线AD翻折（如图2），因为AB＞AC，所以点B落在AC的延长线上的点B'处．于是，由∠ACB＞∠B'，∠ABC=∠B'，可得∠ACB＞∠ABC．

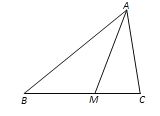
（1）灵活运用：从上面的证法可以看出，折纸常常能为证明一个命题提供思路和方法．由此小明想到可用类似方法证明“大角对大边”：如图3．在△ABC中，如果∠ACB＞∠ABC，那么AB＞AC．小明的思路是：沿BC的垂直平分线翻折……请你帮助小明完成后面的证明过程．

（2）拓展延伸：请运用上述方法或结论解决如下问题：

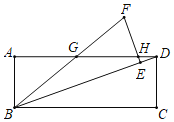
如图4，已知M为正方形ABCD的边CD上一点（不含端点），连接AM并延长，交BC的延长线于点N．求证：AM＋AN＞2BD．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）设BC的中垂线交BC于点E，交AB于点D，连接DC，结合中垂线的性质定理与三角形三边长的关系，即可得到结论；

（2）延长DC到点E，使得CE=CN，连接AE交BC于点F．易证△ACE≌△CAN，得AE=AN．过点C作PQ⊥AC，分别交AN、AE于点P、Q，结合“三角形中，大角对大边”，得AP＋AQ＞2AC，QE＞CQ，PC＞PM，进而得QE＞PM，即AM＋AN＞AP＋AQ，然后即可得到结论．

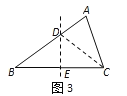
（1）设BC的中垂线交BC于点E，交AB于点D，连接DC．

将∠B沿BC的中垂线DE翻折（如图3），使点B落在点C处．

∵∠ACB＞∠ABC，

∴CD在△ABC的内部，

∵DE为BC的中垂线，

∴DB=DC．

∵在△ADC中，AD＋DC＞AC，

∴AD＋DB＞AC．即AB＞AC；

（2）如图4，延长DC到点E，使得CE=CN，连接AE交BC于点F．

∵∠ACE=∠ACN=135°，CE=CN，AC=AC，

∴△ACE≌△ACN（SAS），

∴AE=AN．

过点C作PQ⊥AC，分别交AN、AE于点P、Q．

∵∠ACP=∠ACQ=90°，

∴AP＞AC，AQ＞AC，

∴AP＋AQ＞2AC．

∵∠ACD＞∠E，∠ACD=45°，∠QCE=135°-90°=45°，

∴∠QCE＞∠E，

∴QE＞CQ．

同理可得：PC＞PM．

∵△ACE≌△ACN，

∴∠CAN=∠CAE，

又∵AC=AC，∠ACP=∠ACQ=90°，

∴△ACP≌△ACQ（ASA），

∴PC=CQ，

∴QE＞PM，

∴AM＋AN=AM＋AE=AM＋AQ＋QE＞AM＋AQ＋PM=AP＋AQ．

又∵AP＋AQ＞2AC，

∴AM＋AN＞2AC．

∵正方形ABCD中，AC=BD，

∴AM＋AN＞2BD．