题目内容
如图,以矩形ABCD的边AB为直径作圆,过C作直线CP切圆于点P,过点P作PQ⊥AB于Q,PQ分别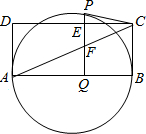 交CD、AC于E、F,记AQ=m,QB=n(m>n).
交CD、AC于E、F,记AQ=m,QB=n(m>n).(1)用含m、n的代数式表示PC的长;
(2)求证:直线AC平分线段PQ.
分析:(1)连接PA、PB,由圆周角定理可以得知∠APB=90°利用三角形相似表示出PQ,在直角三角形PEC中利用勾股定理就可以表示出PC.
(2)由PQ⊥AB及四边形ABCD是矩形可知PQ∥BC,而得到三角形相似证明FQ=
PQ,从而使问题得到解决.
(2)由PQ⊥AB及四边形ABCD是矩形可知PQ∥BC,而得到三角形相似证明FQ=
| 1 |
| 2 |
解答: (1)解:连接PA、PB
(1)解:连接PA、PB
∵AB是直径,
∴∠APB=90°
设CP=x,则CB=CP=x
∵PQ⊥AB
∴△APQ∽△PBQ
∴PQ2=AQ•QB
∴PQ=
∴PE=
-x,又CE=n
在Rt△PCE中有PC2=PE2+EC2
∴x2=(
-x)2+n2
∴x=
;
(2)证明:∵PQ∥CB
∴
=
=
∴FQ=
•CB=
•
=
∴FQ=
PQ
∴直线AC平分线段PQ.
 (1)解:连接PA、PB
(1)解:连接PA、PB∵AB是直径,
∴∠APB=90°
设CP=x,则CB=CP=x
∵PQ⊥AB
∴△APQ∽△PBQ
∴PQ2=AQ•QB
∴PQ=
| mn |
∴PE=
| mn |
在Rt△PCE中有PC2=PE2+EC2
∴x2=(
| mn |
∴x=
(m+n)
| ||
| 2m |
(2)证明:∵PQ∥CB
∴
| FQ |
| CB |
| AQ |
| AB |
| m |
| m+n |
∴FQ=
| m |
| m+n |
| m |
| m+n |
(m+n)
| ||
| 2m |
| ||
| 2 |
∴FQ=
| 1 |
| 2 |
∴直线AC平分线段PQ.
点评:本题考查了切线的性质,勾股定理,矩形的性质,平行线分线段成比例定理及相似三角形的判定及性质的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
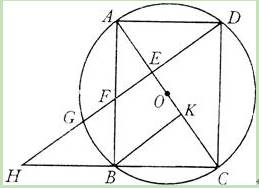
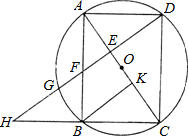 已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.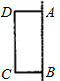 如图,以矩形ABCD的边AB所在直线为轴将其旋转一周,所形成的几何体的俯视图是( )
如图,以矩形ABCD的边AB所在直线为轴将其旋转一周,所形成的几何体的俯视图是( )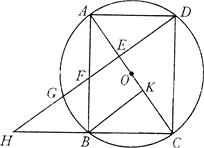
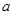 ,AD=
,AD=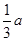 (
(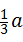 (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长: