题目内容
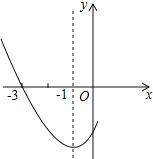
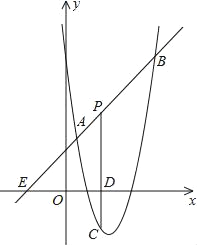
【题目】如图，抛物线y=ax2+bx-4a经过A(-1，0)、C(0，4)两点，与x轴交于另一点B．
（1）求抛物线的解析式；
（2）已知点D(m，m+1)在第一象限的抛物线上，求点D关于直线BC对称的点的坐标；
（3）在（2）的条件下，连接BD，点P为抛物线上一点，且∠DBP=45°，求点P的坐标．
【答案】（1）抛物线的解析式为y=-x2+3x+4；（2）（0，1）；（3）（-
，
）.
【解析】
此题是二次函数的综合题，求解析式、求点的坐标是函数中基本题型，要求学生熟练、准确的解题。
解：（1）
抛物线
经过
，
两点，
解得
抛物线的解析式为
．
（2）点
在抛物线上，
，
即
，
或
．
点
在第一象限，点的坐标为
．
由（1）知
．
设点关于直线
的对称点为点
．
，
，且
，
，
练习册系列答案
相关题目
