题目内容
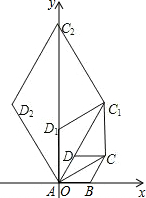 如图,边长为1的菱形ABCD中,A在原点,B在x轴正半轴上,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACC1D1,∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°,…,C、C1、C2、C3…按逆时针方向排列,按此规律所作的第2015个菱形AC2013C2014D2014的顶点C2014的坐标为
如图,边长为1的菱形ABCD中,A在原点,B在x轴正半轴上,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACC1D1,∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°,…,C、C1、C2、C3…按逆时针方向排列,按此规律所作的第2015个菱形AC2013C2014D2014的顶点C2014的坐标为考点:菱形的性质,坐标与图形性质
专题:规律型
分析:连接BD交AC于E,根据菱形的对角线平分一组对角线求出∠BAC=30°,根据菱形的对角线互相垂直平分可得AC⊥BD,然求出AE,再求出AC,从而判断出下一个菱形的边与上一个菱形的边的夹角为30°并且边长为上一个菱形边长的
倍,然后判断出每12个菱形为一个循环组依次循环,再用2015除以12,根据商和余数的情况确定出点C2014的位置与长度,然后解直角三角形并写出点C2014的坐标即可.
| 3 |
解答: 解:如图,连接BD交AC于E,
解:如图,连接BD交AC于E,
∵四边形ABCD是菱形,
∴∠BAC=
∠BAC=
×60°=30°,AC⊥BD,
∴AE=AB•cos30°=
AB,
∴AC=2AE=2×
AB=
×1=
,
同理∠CAC1=30°,AC1=(
)2,
…,
每12个菱形为一个循环组依次循环,且AC2014=(
)2015,
∵2015÷2=167余11,
∴菱形AC2013C2014D2014是第168组的最后一个菱形,AC2014在第四象限,
∵(
)2015×
=
,
(
)2015×
=
,
∴顶点C2014的坐标为(
,-
).
故答案为:(
,-
).
 解:如图,连接BD交AC于E,
解:如图,连接BD交AC于E,∵四边形ABCD是菱形,
∴∠BAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=AB•cos30°=
| ||
| 2 |
∴AC=2AE=2×
| ||
| 2 |
| 3 |
| 3 |
同理∠CAC1=30°,AC1=(
| 3 |
…,
每12个菱形为一个循环组依次循环,且AC2014=(
| 3 |
∵2015÷2=167余11,
∴菱形AC2013C2014D2014是第168组的最后一个菱形,AC2014在第四象限,
∵(
| 3 |
| ||
| 2 |
(
| ||
| 2 |
(
| 3 |
| 1 |
| 2 |
(
| ||
| 2 |
∴顶点C2014的坐标为(
(
| ||
| 2 |
(
| ||
| 2 |
故答案为:(
(
| ||
| 2 |
(
| ||
| 2 |
点评:本题考查了菱形的性质,解直角三角形,锐角三角函数,熟记性质并求出菱形的边的规律性变化是解题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、过直线外一点有且仅有一条直线与它平行 |
| B、在同一平面内,不同的两条直线只有一个交点 |
| C、经过一点有且只有一条直线与已知直线垂直 |
| D、经过两点有且只有一条直线 |
 如图,AB∥CD,DB⊥BC,∠1=50°,则∠2的度数等于
如图,AB∥CD,DB⊥BC,∠1=50°,则∠2的度数等于 如图,Rt△ABO的斜边OA在x轴上,点B在第一象限内,OA:OB=5:4,边AB的垂直平分线分别交 AB、x轴于点C、D,线段CD交反比例函数
如图,Rt△ABO的斜边OA在x轴上,点B在第一象限内,OA:OB=5:4,边AB的垂直平分线分别交 AB、x轴于点C、D,线段CD交反比例函数