题目内容
如图,在等腰直角三角形ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的 一点,且PB=PD,DE⊥AC,垂足为点E.
一点,且PB=PD,DE⊥AC,垂足为点E.(1)求证:PE=BO;
(2)设AC=2a,AP=x,四边形PBDE的面积为y,求y与x之间的函数关系式,并写出自变量的取值范围.
分析:(1)根据条件可证明Rt△BOP≌Rt△PDE,所以,BO=PE;
(2)PE=AO=BO=OC=a,AP=x,EC=DE=OP=AO-AP=a-x,BC=AB=
a,作EF⊥CD,EF=EC•
,所以可求得y=S△BPO+S△BOC-
S△DOE=a2-
-
,(0≤x≤a).
(2)PE=AO=BO=OC=a,AP=x,EC=DE=OP=AO-AP=a-x,BC=AB=
| 2 |
| ||
| 2 |
S△DOE=a2-
| ax |
| 2 |
| (a-x)2 |
| 2 |
解答:(1)证明:∠PDB=∠PBD=45°+∠PBO=45°+∠DPC(∠PDB外角)
∴∠PBO=∠DPC.
又∵BP=DP
∴Rt△BOP≌Rt△PDE
∴BO=PE;
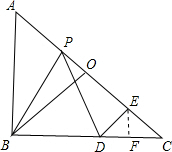
(2)解:PE=AO=BO=OC=a,AP=x
EC=DE=OP=AO-AP=a-x
BC=AB=
a
作EF⊥CD,EF=EC•
y=S△BPO+S△BOC-S△DCE
=
+
-
=a2-
-
.(0≤x≤a).
∴∠PBO=∠DPC.
又∵BP=DP
∴Rt△BOP≌Rt△PDE
∴BO=PE;

(2)解:PE=AO=BO=OC=a,AP=x
EC=DE=OP=AO-AP=a-x
BC=AB=
| 2 |
作EF⊥CD,EF=EC•
| ||
| 2 |
y=S△BPO+S△BOC-S△DCE
=
| a2 |
| 2 |
| a(a-x) |
| 2 |
| (a-x)2 |
| 2 |
| ax |
| 2 |
| (a-x)2 |
| 2 |
点评:主要考查了二次函数的综合运用,利用全等三角形判定和性质求出相等的线段再利用线段的和差关系表示出所求图形的边长及相关线段,利用面积公式求面积是解题的关键.

练习册系列答案
相关题目
教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:

(1)sad 的值为( ▼ )
的值为( ▼ )
(2)对于 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .
(3)已知 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A=
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:

(1)sad
 的值为( ▼ )
的值为( ▼ )A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为( ▼ )
的值为( ▼ )
A. | B.1 | C. | D.2 |
 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .(3)已知
 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值. 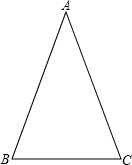 互唯一确定的.
互唯一确定的.
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
 的值为( ▼ )
的值为( ▼ ) B.
1 C.
B.
1 C.  D.
2
D.
2 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ . ,其中
,其中 为锐角,试求sad
为锐角,试求sad