Question

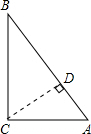
△ABC中，∠C=90°，AC=3，AB=6，以C为圆心，R为半径作⊙C，则线段AB与⊙C相离时，R的取值范围是________；相切时，R的取值范围是________；相交时，R的取值范围是________．

Answer 1

        
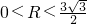
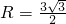
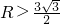
分析：（1）当线段AB与⊙C相离时，即C到AB的距离d大于⊙C的半径r，d＞r；
（2）当线段AB与⊙C相切时，即C到AB的距离d等于⊙C的半径r，d=r；
（3）当线段AB与⊙C相交时，即C到AB的距离d等于⊙C的半径r，d＜r．
解答：过作CD⊥AB于D，在Rt△ABC中，AC=3，AB=6，∴BC=3，
∴CD=d==，
∵当直线AB与⊙C相离时，d＞r，
∴0＜r＜；
∵当直线AB与⊙C相切时，d=r，
∴r=；
∵当直线AB与⊙C相交时，d＜r，
∴r＞，
故答案为：0＜R＜；R=；R＞．
点评：本题考查直线与圆的位置关系，若圆的半径为r，圆心到直线的距离为d，d＞r时，圆和直线相离；d=r时，圆和直线相切；d＜r时，圆和直线相交．