题目内容
已知如图：⊙O的半径为8cm，把弧AmB沿AB折叠使弧AmB经过圆心O，再把弧AOB沿CD折叠，使弧COD经过AB的中点E，则折线CD的长为（ ）
A．8cm
B．8
cmC．2
cmD．4
cm
【答案】分析：连接OE并延长交CD于点F，交C′D′于点F′，交弧AmB于点G，根据翻折的性质得出OF′=6，再由勾股定理得出．
解答：解：连接OE并延长交CD于点F，交C′D′于点F′，交弧AmB于点G，
∵OC′=8cm，
∴OF′=6cm，
∴C′F′=CF=
=2
cm，
F∴CD=2CD=4
cm．
故选D．
点评：本题考查了垂径定理和勾股定理以及翻折的性质，是基础知识要熟练掌握．
解答：解：连接OE并延长交CD于点F，交C′D′于点F′，交弧AmB于点G，
∵OC′=8cm，
∴OF′=6cm，
∴C′F′=CF=
=2cm，F∴CD=2CD=4
cm．故选D．
点评：本题考查了垂径定理和勾股定理以及翻折的性质，是基础知识要熟练掌握．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知如图，圆锥的底面圆的半径为r（r＞0），母线长OA为3r，C为母线OB的中点在圆锥的侧面上，一只蚂蚁从点A爬行到点C的最短线路长为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
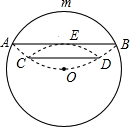已知如图：⊙O的半径为8cm，把弧AmB沿AB折叠使弧AmB经过圆心O，再把弧AOB沿CD折叠，使弧COD经过AB的中点E，则折线CD的长为（ ）| A、8cm | ||
B、8
| ||
C、2
| ||
D、4
|
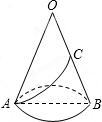已知如图，圆锥的底面圆的半径为r（r＞0），母线长OA为2r，C为母线OB的中点．在圆锥的侧面上，一只蚂蚁从点A爬行到点C的最短线路长为
已知如图：⊙O的半径为8cm，把弧AmB沿AB折叠使弧AmB经过圆心O，再把弧AOB沿CD折叠，使弧COD经过AB的中点E，则折线CD的长为
cm
cm