题目内容
对于抛物线y=-ax2+2ax-a(a≠0),下列叙述错误的是( )
| A、对称轴是直线x=1 | B、与y轴交于(0,-a) | C、与x轴只有一个公共点 | D、函数有最大值 |
分析:A、可直接根据抛物线的对称轴方程x=-
进行判断;
B、考查的是二次函数与坐标轴交点坐标的求法,令x=0,可求出抛物线与y轴的交点坐标;令y=0,可求出抛物线与x轴交点坐标;
C、用根的判别式进行判断即可;
D、首先要确定抛物线的开口方向,再判断函数是否有最大值.
| b |
| 2a |
B、考查的是二次函数与坐标轴交点坐标的求法,令x=0,可求出抛物线与y轴的交点坐标;令y=0,可求出抛物线与x轴交点坐标;
C、用根的判别式进行判断即可;
D、首先要确定抛物线的开口方向,再判断函数是否有最大值.
解答:解:A、抛物线的对称轴为x=-
=-(-1)=1;故A正确;
B、令x=0,则y=-a;所以抛物线与y轴的交点为(0,-a);故B正确;
C、令y=0,则-ax2+2ax-a=0,△=(2a)2-4a2=0,所以此抛物线与x轴只有一个公共点,故C正确;
D、由于a的符号不确定,当a<0时,抛物线开口向上,有最小值,故D错误.
故选D.
| 2a |
| -2a |
B、令x=0,则y=-a;所以抛物线与y轴的交点为(0,-a);故B正确;
C、令y=0,则-ax2+2ax-a=0,△=(2a)2-4a2=0,所以此抛物线与x轴只有一个公共点,故C正确;
D、由于a的符号不确定,当a<0时,抛物线开口向上,有最小值,故D错误.
故选D.
点评:此题考查了二次函数的相关性质,要求熟练掌握对称轴公式、与坐标轴交点坐标的求法,会用a值判断开口方向,能根据函数解析式判断与x轴交点坐标的个数.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
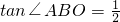 ,求抛物线的解析式;
,求抛物线的解析式; ,求抛物线的解析式;
,求抛物线的解析式; (其中a为常数,且a>0)
(其中a为常数,且a>0)
 时,设
时,设 与x轴分别交于M、N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E、F两点(E在F的左边),观察M、N、E、F四点坐标,请写出一个你所得到的正确结论,并说明理由。
与x轴分别交于M、N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E、F两点(E在F的左边),观察M、N、E、F四点坐标,请写出一个你所得到的正确结论,并说明理由。  都垂直于x轴,
都垂直于x轴, 分别经过A、B两点,在直线
分别经过A、B两点,在直线 之间,且与两条抛物线分别交于C、D两点,求线段CD长的最大值。
之间,且与两条抛物线分别交于C、D两点,求线段CD长的最大值。