题目内容
如果|a|=4,|b|=2,且|a+b|=a+b,则a-b的值是 .
考点:绝对值
专题:分类讨论
分析:首先根据绝对值的意义求得a,b的值,再由|a+b|=a+b确定出a与b的对应值有两种可能性,然后分别代入a-b,根据有理数的减法法则计算即可.
解答:解:∵|a|=4,|b|=2,
∴a=±4,b=±2,
∵|a+b|=a+b,
∴a+b>0,
∴a、b同正即a=4,b=2,或a=4,b=-2.
当a=4,b=2时,a-b=4-2=2;
当a=4,b=-2时,a-b=4-(-2)=4+2=6.
故a-b的值为:2或6.
∴a=±4,b=±2,
∵|a+b|=a+b,
∴a+b>0,
∴a、b同正即a=4,b=2,或a=4,b=-2.
当a=4,b=2时,a-b=4-2=2;
当a=4,b=-2时,a-b=4-(-2)=4+2=6.
故a-b的值为:2或6.
点评:本题考查了有理数的减法,绝对值的性质,难点在于确定出a、b的对应情况.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
|-
|=( )
| 2 |
| 11 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
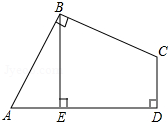 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD,垂足为E.
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD,垂足为E. 如图,在∠1、∠2、∠3中,
如图,在∠1、∠2、∠3中,