Question

求直线y=2x+8，y=-2x-4与y轴所围成的图形的面积．

Answer 1

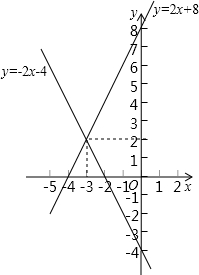解：令x=0，则y=8，所以，直线y=2x+8与y轴的交点坐标为（0，8），
令x=0，则y=-4，所以，直线y=-2x-4与y轴的交点坐标为（0，-4），
联立，
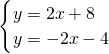解得，
所以，两直线的交点坐标是（-3，2），
两直线与y轴所围成的图形的面积S=（8+4）×3=18．
分析：求出两直线与y轴的交点坐标，再联立两直线解析式求出交点坐标，然后根据三角形的面积公式列式计算即可得解．
点评：本题考查了两直线相交的问题，联立两直线解析式，解方程组求交点坐标是常用的方法，一定要熟练掌握并灵活运用．